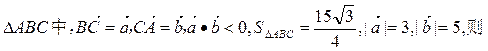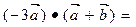题目内容
(本小题满分12分)在△ABC中,a,b,c分别是角A、B、C的对边,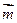 =(2b-c,cosC),
=(2b-c,cosC),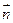 =(a,cosA),且
=(a,cosA),且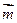 //
//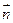 .
.
(Ⅰ)求角A的大小;
(Ⅱ)求值:sin(A-10°)[1+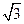 tan(A-50°)];
tan(A-50°)];
(Ⅲ)若a=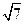 ,
,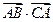 +3=0,b<c,求b和c的值.
+3=0,b<c,求b和c的值.
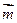 =(2b-c,cosC),
=(2b-c,cosC),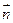 =(a,cosA),且
=(a,cosA),且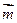 //
//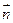 .
.(Ⅰ)求角A的大小;
(Ⅱ)求值:sin(A-10°)[1+
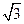 tan(A-50°)];
tan(A-50°)];(Ⅲ)若a=
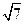 ,
,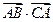 +3=0,b<c,求b和c的值.
+3=0,b<c,求b和c的值.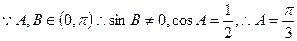 ,1,b=2,c=3
,1,b=2,c=3(Ⅰ)由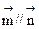 得
得 …………………… 2分
…………………… 2分
由正弦定理得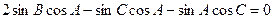
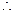
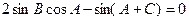
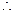
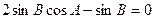 …………………… 4分
…………………… 4分
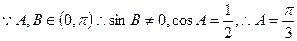 …………………… 5分
…………………… 5分
(Ⅱ) sin(A-10°)[1+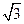 tan(A-50°)]=
tan(A-50°)]= =1…………………… 8分
=1…………………… 8分
(Ⅲ)由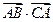 +3=0得,-bccosA+3=0,即bc="6 " ①…………………… 9分
+3=0得,-bccosA+3=0,即bc="6 " ①…………………… 9分
∴7=b2+c2-2bccosA=b2+c2-6,b2+c2="13 " ②…………………… 11分
∵b<c,∴联解①②得b=2,c="3 " …………………… 12分
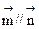 得
得 …………………… 2分
…………………… 2分由正弦定理得
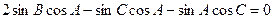
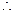
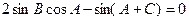
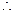
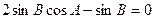 …………………… 4分
…………………… 4分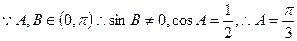 …………………… 5分
…………………… 5分(Ⅱ) sin(A-10°)[1+
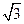 tan(A-50°)]=
tan(A-50°)]= =1…………………… 8分
=1…………………… 8分(Ⅲ)由
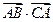 +3=0得,-bccosA+3=0,即bc="6 " ①…………………… 9分
+3=0得,-bccosA+3=0,即bc="6 " ①…………………… 9分∴7=b2+c2-2bccosA=b2+c2-6,b2+c2="13 " ②…………………… 11分
∵b<c,∴联解①②得b=2,c="3 " …………………… 12分

练习册系列答案
相关题目
 海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,问此舰有没有触礁的危险(10分)
海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,问此舰有没有触礁的危险(10分)
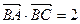 ,且
,且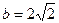 ,求
,求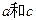 的值.
的值. 中,A=
中,A= ,
, =______
=______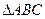 中,a=15,b=10,A=60°,则
中,a=15,b=10,A=60°,则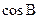 =( )
=( )

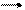 AB=a,
AB=a,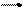 BC=b,
BC=b, CA=c,若a·(a+b
CA=c,若a·(a+b )<0,则△ABC是( )
)<0,则△ABC是( ) 角三角形
角三角形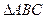 是锐角三角形,
是锐角三角形,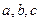 分
分 别是内角
别是内角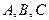 所对边长,且
所对边长,且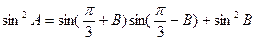
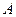 的值;
的值;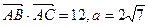 ,求
,求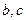 (其中
(其中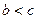 )。
)。