题目内容
用秦九韶方法求多项式 在
在 的值时,
的值时,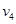 的值为 ( )
的值为 ( )
 在
在 的值时,
的值时,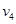 的值为 ( )
的值为 ( )A. | B.220 | C. | D.3392 |
B
首先把一个n次多项式f(x)写成(…((a[n]x+a[n-1])x+a[n-2])x+…+a[1])x+a[0]的形式,然后化简,求n次多项式f(x)的值就转化为求n个一次多项式的值,求出V4的值.
解答:解:∵f(x)=12+35x-8x2+79x3+6x4+5x5+3x6
=(((((3x+5)x+6)x+79)x-8)x+35)x+12,
∴v0=a6=3,
v1=v0x+a5=3×(-4)+5=-7,
v2=v1x+a4=-7×(-4)+6=34,
v3=v2x+a3=34×(-4)+79=-57,
v4=v3x+a2=-57×(-4)+(-8)=220.
故答案为B.
解答:解:∵f(x)=12+35x-8x2+79x3+6x4+5x5+3x6
=(((((3x+5)x+6)x+79)x-8)x+35)x+12,
∴v0=a6=3,
v1=v0x+a5=3×(-4)+5=-7,
v2=v1x+a4=-7×(-4)+6=34,
v3=v2x+a3=34×(-4)+79=-57,
v4=v3x+a2=-57×(-4)+(-8)=220.
故答案为B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,当x=2时的值的过程中,要经过 次乘法运算和 次加法运算。
,当x=2时的值的过程中,要经过 次乘法运算和 次加法运算。



 在x=5时所对应的
在x=5时所对应的 的值为( )
的值为( ) ,
, )
) 化为
化为 进制的数
进制的数 
 }
}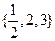

 .5 C.6 D.7
.5 C.6 D.7