题目内容
已知某类学习任务的掌握程度y与学习时间t(单位时间)之间的关系为y=f(t)= ,这里我们称这一函数关系为“学习曲线”.已知这类学习任务中的某项任务有如下两组数据:t=4,y=50%;t=8,y=80%.
,这里我们称这一函数关系为“学习曲线”.已知这类学习任务中的某项任务有如下两组数据:t=4,y=50%;t=8,y=80%.
(Ⅰ)试确定该项学习任务的“学习曲线”的关系式f(t);
(Ⅱ)若定义在区间[x1,x2]上的平均学习效率为 ,问这项学习任务从哪一刻开始的2个单位时间内平均学习效率最高.
,问这项学习任务从哪一刻开始的2个单位时间内平均学习效率最高.
解:(Ⅰ)由题意得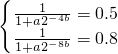 ,
,
整理得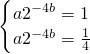 ,解得a=4,b=0.5,
,解得a=4,b=0.5,
所以“学习曲线”的关系式为 .
.
(Ⅱ)设从第x个单位时间起的2个单位时间内的平均学习效率为η,则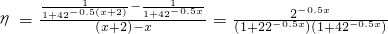
令u=2-0.5x,则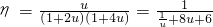 ,
,
显然当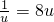 ,即
,即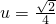 时,η最大,
时,η最大,
将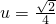 代入u=2-0.5x,得x=3,
代入u=2-0.5x,得x=3,
所以,在从第3个单位时间起的2个单位时间内的平均学习效率最高.
分析:(Ⅰ)由题意得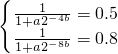 ,由此能求出“学习曲线”的关系式.
,由此能求出“学习曲线”的关系式.
(Ⅱ)设从第x个单位时间起的2个单位时间内的平均学习效率为η,令u=2-0.5x,能推导出在从第3个单位时间起的2个单位时间内的平均学习效率最高.
点评:本题考查函数在生产生活中的实际应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
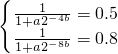 ,
,整理得
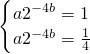 ,解得a=4,b=0.5,
,解得a=4,b=0.5,所以“学习曲线”的关系式为
 .
.(Ⅱ)设从第x个单位时间起的2个单位时间内的平均学习效率为η,则
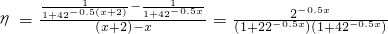
令u=2-0.5x,则
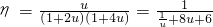 ,
,显然当
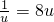 ,即
,即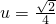 时,η最大,
时,η最大,将
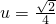 代入u=2-0.5x,得x=3,
代入u=2-0.5x,得x=3,所以,在从第3个单位时间起的2个单位时间内的平均学习效率最高.
分析:(Ⅰ)由题意得
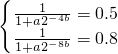 ,由此能求出“学习曲线”的关系式.
,由此能求出“学习曲线”的关系式.(Ⅱ)设从第x个单位时间起的2个单位时间内的平均学习效率为η,令u=2-0.5x,能推导出在从第3个单位时间起的2个单位时间内的平均学习效率最高.
点评:本题考查函数在生产生活中的实际应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
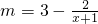 .已知2008年生产该产品m万件的成本C=16m+8万元,厂家将每件产品的销售价定为每件产品成本的1.5倍.
.已知2008年生产该产品m万件的成本C=16m+8万元,厂家将每件产品的销售价定为每件产品成本的1.5倍.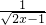 的定义域为B,求
的定义域为B,求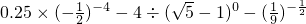 .
.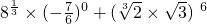 .
.