题目内容
已知p(p≥2)是给定的某个正整数,数列{an}满足:a1=1,(k+1)ak+1=p(k-p)ak,其中k=1,2,3,…,p-1.
(I)设p=4,求a2,a3,a4;
(II)求a1+a2+a3+…+ap.
解:(Ⅰ)由(k+1)ak+1=p(k-p)ak得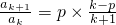 ,k=1,2,3,…,p-1
,k=1,2,3,…,p-1
即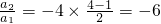 ,a2=-6a1=-6;
,a2=-6a1=-6;
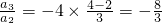 ,a3=16,
,a3=16,
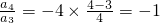 ,a4=-16; (3分)
,a4=-16; (3分)
(Ⅱ)由(k+1)ak+1=p(k-p)ak
得: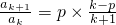 ,k=1,2,3,…,p-1
,k=1,2,3,…,p-1
即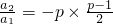 ,
,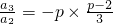 ,…,
,…,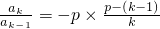 ,
,
以上各式相乘得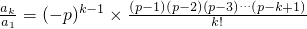 (5分)
(5分)
∴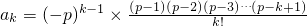
=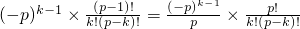
= ,k=1,2,3,…,p (7分)
,k=1,2,3,…,p (7分)
∴a1+a2+a3+…+ap=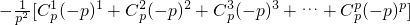 =
=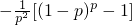 (10分)
(10分)
分析:(I)设p=4,利用(k+1)ak+1=p(k-p)ak,求出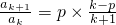 ,通过k=1,2,3求a2,a3,a4;
,通过k=1,2,3求a2,a3,a4;
(II)利用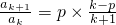 列出
列出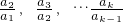 的表达式通过连乘求出ak,然后通过二项式定理求解求a1+a2+a3+…+ap.
的表达式通过连乘求出ak,然后通过二项式定理求解求a1+a2+a3+…+ap.
点评:本题考查数列的应用,数列的项的求法,通项公式的求法,二项式定理的应用,考查转化思想计算能力.
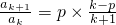 ,k=1,2,3,…,p-1
,k=1,2,3,…,p-1即
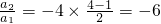 ,a2=-6a1=-6;
,a2=-6a1=-6;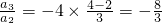 ,a3=16,
,a3=16,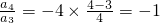 ,a4=-16; (3分)
,a4=-16; (3分)(Ⅱ)由(k+1)ak+1=p(k-p)ak
得:
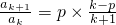 ,k=1,2,3,…,p-1
,k=1,2,3,…,p-1即
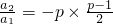 ,
,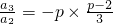 ,…,
,…,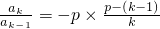 ,
,以上各式相乘得
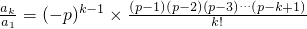 (5分)
(5分)∴
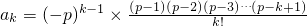
=
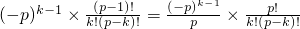
=
 ,k=1,2,3,…,p (7分)
,k=1,2,3,…,p (7分)∴a1+a2+a3+…+ap=
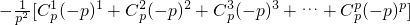 =
=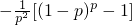 (10分)
(10分)分析:(I)设p=4,利用(k+1)ak+1=p(k-p)ak,求出
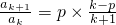 ,通过k=1,2,3求a2,a3,a4;
,通过k=1,2,3求a2,a3,a4;(II)利用
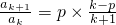 列出
列出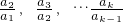 的表达式通过连乘求出ak,然后通过二项式定理求解求a1+a2+a3+…+ap.
的表达式通过连乘求出ak,然后通过二项式定理求解求a1+a2+a3+…+ap.点评:本题考查数列的应用,数列的项的求法,通项公式的求法,二项式定理的应用,考查转化思想计算能力.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目