题目内容
函数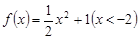 的反函数是( )
的反函数是( )
A. . . | B. . . |
C. . . | D. . . |
D
解析试题分析:求反函数,除了求解析式以外,还要求出定义域,即原函数的值域.由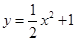 得
得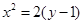 ,又
,又 ,所以
,所以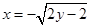 ,另外当
,另外当 时,
时,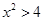 ,
,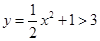 ,因此所求反函数为D.
,因此所求反函数为D.
考点:求反函数.

练习册系列答案
相关题目
设f(x)为定义在R上的奇函数,当x≥0时,f(x)= +2x+m (m为常数),则
+2x+m (m为常数),则 ( )
( )
| A.3 | B.1 | C. | D. |
已知函数 的导函数
的导函数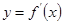 的图象如图所示,则关于函数
的图象如图所示,则关于函数 ,下列说法正确的是 ( )
,下列说法正确的是 ( )
A.在 处取得最大值 处取得最大值 | B.在区间 上是增函数 上是增函数 |
C.在区间 上函数值均小于0 上函数值均小于0 | D.在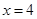 处取得极大值 处取得极大值 |
函数 在
在 上是增函数,则实数
上是增函数,则实数 的范围是( )
的范围是( )
A. ≥ ≥ | B. ≥ ≥ | C. ≤ ≤ | D. ≤ ≤ |
已知函数f(x)是R上的单调递增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A.恒为正数 |
| B.恒为负数 |
| C.恒为0 |
| D.可以为正数也可以为负数 |
同时满足两个条件:①定义域内是减函数;②定义域内是奇函数的函数是( ).
| A.f(x)=-x|x| | B.f(x)=x3 |
| C.f(x)=sin x | D.f(x)= |
函数f(x)= ( ).
( ).
A.在 上递增 上递增 |
B.在 上递增,在 上递增,在 上递减 上递减 |
C.在 上递减 上递减 |
D.在 上递减,在 上递减,在 上递增 上递增 |
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)= ,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
A.0<k≤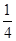 或k= 或k= | B.0<k≤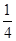 |
C.0<k<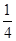 或k= 或k= | D.0<k<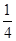 |
