题目内容
(本题满分12分)
一个多面体的三视图及直观图如右图所示:
(Ⅰ)求异面直线AB1与DD1所成角的余弦值:
(Ⅱ)试在平面ADD1A1中确定一个点F,使得FB1⊥平面BCC1B1;
(Ⅲ)在(Ⅱ)的条件下,求二面角F―CC1―B的余弦值.
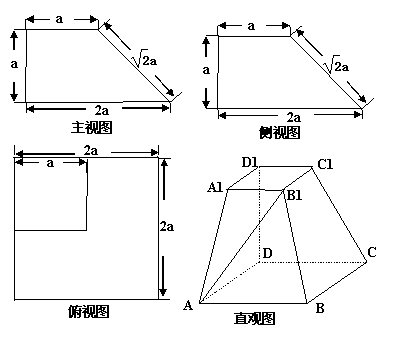
解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD。
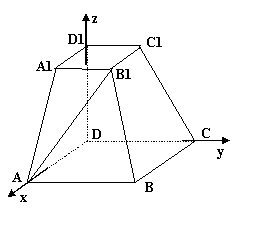 AB=2A1B1=2DD1=2a……………2分以D为原点,DA、DC、DD1所在的直线为X,Y,Z轴,
AB=2A1B1=2DD1=2a……………2分以D为原点,DA、DC、DD1所在的直线为X,Y,Z轴,
建立如图所示的空间直角坐标系,则D(0,0,0),
A(2a,0,0),B1(a,a,a),D1(0,0,a),
B(2a,2a,0),C(0,2a,0),C1(0,a,a)…4分
(Ⅰ)![]()
![]()

即直线AB1与DD1所成角的余弦值为![]() ………………………………………………6分
………………………………………………6分
(II)设F(x,0,z),![]()
![]() 由FB1
由FB1![]() 平面BCC1B1得
平面BCC1B1得
即 得
得![]()
![]() 即F为DA的中点…………9分
即F为DA的中点…………9分
(III)由(II)知FB1为平面BCC1B1的法向量。
设![]() 为平面FCC1的法向量。
为平面FCC1的法向量。![]()
由 即
即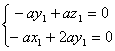 令y1=1得x1=2,z1=1
令y1=1得x1=2,z1=1

即二面角F―CC1―B的余弦值为![]() …………………………………12分
…………………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面