题目内容
(12分)设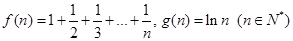 。
。
(1)设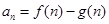 ,求
,求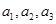 ,并证明
,并证明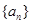 为递减数列;
为递减数列;
(2)是否存在常数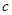 ,使
,使 对
对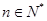 恒成立?若存在,试找出
恒成立?若存在,试找出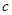 的一个值,并证明;若不存在,说明理由。
的一个值,并证明;若不存在,说明理由。
【答案】
(1)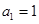 .
. 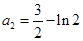 ,
, 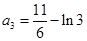 .证明见解析
.证明见解析
(2)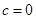
【解析】(1)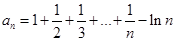 .由此
.由此
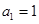 .
.
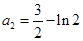 ,
,
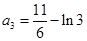 .
.
又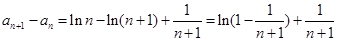 .
.
构造函数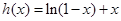 .
. 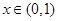
由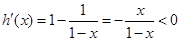
知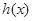 在
在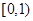 上为单减函数.
上为单减函数.
从而当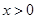 时,
时,
取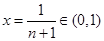 .有
.有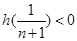
即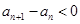
故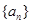 为递减数列.
为递减数列.
(2)存在如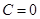 等,下证
等,下证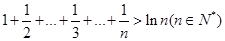
注意到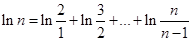 .
.
这只要证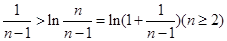 即可.
即可.
容易证明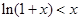 对
对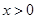 恒成立.(这里略)
恒成立.(这里略)
取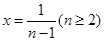 即可得上式成立.
即可得上式成立.
从而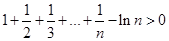
此时常数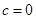 .
.

练习册系列答案
相关题目
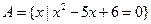 ,
,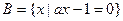 .
.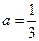 ,试判定集合
,试判定集合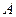 与
与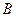 的关系;
的关系;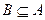 ,求实数
,求实数 的取值组成的集合
的取值组成的集合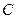 .
.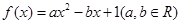 ,
,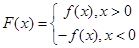
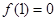 且对任意实数
且对任意实数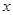 均有
均有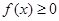 ,求
,求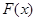 的解析式;
的解析式;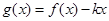 在区间
在区间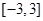 是单调函数,求实数
是单调函数,求实数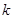 的取值范围;
的取值范围; 且
且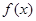 为偶函数,如果
为偶函数,如果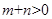 ,求证:
,求证: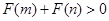 .
.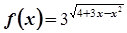

 ,讨论函数
,讨论函数 的单调性;
的单调性; 成立,求实数
成立,求实数 的取值范围。
的取值范围。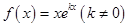
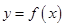 在点
在点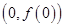 处的切线方程。
处的切线方程。 在区间
在区间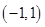 内单调递增,求
内单调递增,求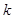 的取值范围。
的取值范围。