题目内容
选修4-4:坐标系与参数方程选讲.在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为(2,
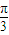 ).
).(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线l(3)的参数方程为
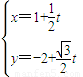 (t为参数),直线l与圆C相交于A,B两点,已知定点M(1,-2),求|MA|•|MB|.
(t为参数),直线l与圆C相交于A,B两点,已知定点M(1,-2),求|MA|•|MB|.
【答案】分析:(1)设点P(ρ,θ)是圆C上的任意一点,根据|OP|=2|OC|cos∠COP 求得圆C的极坐标方程.
(2)先求出圆C的直角坐标方程,把直线l的参数方程与圆的方程联立方程组,化为关于t的一元二次方程,
利用根与系数的关系以及参数的几何意义,求出|MA|•|MB|.
解答:解:(1)设点P(ρ,θ)是圆C上的任意一点,则在△COP中,OC=2,OP=ρ,∠COP=|θ-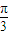 |.
|.
而|OP|=2|OC|cos∠COP,∴ρ=4cos(θ-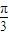 ),即为所求的圆C的极坐标方程.
),即为所求的圆C的极坐标方程.
(2)圆心的直角坐标为(2cos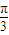 ,2sin
,2sin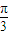 ),即 C(1,
),即 C(1,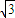 ),故圆C的直角坐标方程为 (x-1)2+(y-
),故圆C的直角坐标方程为 (x-1)2+(y-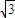 )2=4.
)2=4.
把直线l的参数方程与圆的方程联立方程组,化简可得 t2-(3+2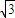 )t+4
)t+4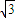 =0,∴t1•t2=3+4
=0,∴t1•t2=3+4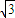 .
.
再根据参数的几何意义可得|MA|•|MB|=|t1•t2|=3+4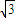 .
.
点评:本题主要考查点的极坐标与直角坐标的互化,一元二次方程根与系数的关系,参数的几何意义,属于基础题.
(2)先求出圆C的直角坐标方程,把直线l的参数方程与圆的方程联立方程组,化为关于t的一元二次方程,
利用根与系数的关系以及参数的几何意义,求出|MA|•|MB|.
解答:解:(1)设点P(ρ,θ)是圆C上的任意一点,则在△COP中,OC=2,OP=ρ,∠COP=|θ-
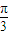 |.
|.而|OP|=2|OC|cos∠COP,∴ρ=4cos(θ-
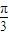 ),即为所求的圆C的极坐标方程.
),即为所求的圆C的极坐标方程.(2)圆心的直角坐标为(2cos
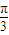 ,2sin
,2sin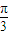 ),即 C(1,
),即 C(1,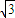 ),故圆C的直角坐标方程为 (x-1)2+(y-
),故圆C的直角坐标方程为 (x-1)2+(y-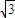 )2=4.
)2=4.把直线l的参数方程与圆的方程联立方程组,化简可得 t2-(3+2
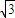 )t+4
)t+4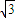 =0,∴t1•t2=3+4
=0,∴t1•t2=3+4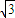 .
.再根据参数的几何意义可得|MA|•|MB|=|t1•t2|=3+4
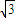 .
.点评:本题主要考查点的极坐标与直角坐标的互化,一元二次方程根与系数的关系,参数的几何意义,属于基础题.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲