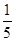题目内容
一个口袋中装有2个白球和n个红球(n≥2且n∈n*),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(Ⅰ) 摸球一次,若中奖概率为 ,求n的值;
,求n的值;
(Ⅱ) 若n=3,摸球三次,记中奖的次数为ξ,试写出ξ的分布列并求其期望.
解:(I)一次摸球从n+2个球中任选两个,有Cn+22种选法,其中两球颜色相同有Cn2+C22种选法;
一次摸球中奖的概率P=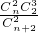 =
=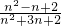 ;
;
由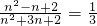 得n=2;
得n=2;
(II)由题意知若n=3,则每次摸球中奖的概率为p=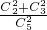 =
= ,且ξ~B(3,
,且ξ~B(3, )
)
所以ξ的期望为Eξ=n×p= .
.
分析:(I)求出一次摸球从n+2个球中任选两个方法,两球颜色相同有Cn2+C22种选法,即可求出摸球中奖的概率P,再由p= 即可求n的值;
即可求n的值;
(II)由题意知若n=3,求得每次摸球中奖的概率 ,根据ξ~B(3,
,根据ξ~B(3, ),Eξ=n×p,即可求出ξ的期望.
),Eξ=n×p,即可求出ξ的期望.
点评:本题考查组合及组合数公式,等可能事件的概率,离散型随机变量期望.求离散型随机变量期望的步骤:①确定离散型随机变量 的取值.②写出分布列,并检查分布列的正确与否,即看一下所有概率的和是否为1.③求出期望.
一次摸球中奖的概率P=
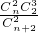 =
=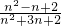 ;
;由
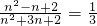 得n=2;
得n=2;(II)由题意知若n=3,则每次摸球中奖的概率为p=
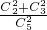 =
= ,且ξ~B(3,
,且ξ~B(3, )
)所以ξ的期望为Eξ=n×p=
 .
.分析:(I)求出一次摸球从n+2个球中任选两个方法,两球颜色相同有Cn2+C22种选法,即可求出摸球中奖的概率P,再由p=
 即可求n的值;
即可求n的值;(II)由题意知若n=3,求得每次摸球中奖的概率
 ,根据ξ~B(3,
,根据ξ~B(3, ),Eξ=n×p,即可求出ξ的期望.
),Eξ=n×p,即可求出ξ的期望.点评:本题考查组合及组合数公式,等可能事件的概率,离散型随机变量期望.求离散型随机变量期望的步骤:①确定离散型随机变量 的取值.②写出分布列,并检查分布列的正确与否,即看一下所有概率的和是否为1.③求出期望.

练习册系列答案
相关题目
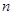 个红球(
个红球( 且
且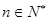 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖. 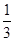 ,求
,求 的值;
的值;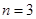 ,摸球三次,记中奖的次数为
,摸球三次,记中奖的次数为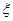 ,试写出
,试写出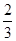 B.
B.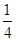 C.
C.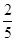 D.
D.