题目内容
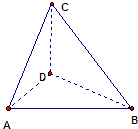 设Rt△ABC斜边AB上的高是CD,AC=BC=2,沿高CD作折痕将之折成直二面角A-CD-B(如图)那么得到二面角C-AB-D的余弦值等于( )
设Rt△ABC斜边AB上的高是CD,AC=BC=2,沿高CD作折痕将之折成直二面角A-CD-B(如图)那么得到二面角C-AB-D的余弦值等于( )分析:利用直角三角形的勾股定理求出AD,BD,CD的长度,取AB的中点E,连接CE,DE,判断出∠CED为二面角C-AB-D的平面角
,然后通过解直角三角形求出二面角的大小.
,然后通过解直角三角形求出二面角的大小.
解答:解:因为Rt△ABC斜边AB上的高是CD,AC=BC=2,
所以CD⊥AD,CD⊥BD,AD=BD=
,CD=
所以CD⊥平面ABD
取AB的中点E,连接CE,DE,
因为AC=BC=2,所以CE⊥AB,DE⊥AB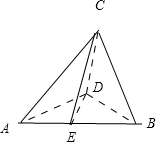
所以∠CED为二面角C-AB-D的平面角
在△ADB中,DE=
=1,CE=
=
=
在Rt△CDE中,cos∠CED=
=
=
故选B.
所以CD⊥AD,CD⊥BD,AD=BD=
| 2 |
所以CD⊥平面ABD
取AB的中点E,连接CE,DE,
因为AC=BC=2,所以CE⊥AB,DE⊥AB

所以∠CED为二面角C-AB-D的平面角
在△ADB中,DE=
| ||||
| 2 |
| CD2+DE2 |
| 2+1 |
| 3 |
在Rt△CDE中,cos∠CED=
| DE |
| CE |
| 1 | ||
|
| ||
| 3 |
故选B.
点评:本题考查求二面角的大小,一般先找出平面角,再证明,再解三角形,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
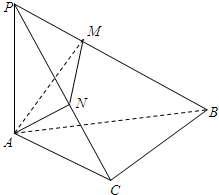 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
 ,(
,(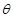 为常数,
为常数,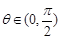 )交于
)交于 两点,则
两点,则