题目内容
袋中装有大小相等的3个白球,2个红球和n个黑球,现从中任取2个球,每取得一个白球得1分,每取得一个红球得2分,每取得一个黑球0分,用ξ表示所得分数,已知得0分的概率为 .
.
(Ⅰ)袋中黑球的个数n;
(2)ξ的概率分布列及数学期望Eξ.
(3)求在取得两个球中有一个是红球的条件下,求另一个是黑球的概率.
解:(1)∵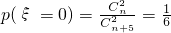 ,…(3分)
,…(3分)
∴n2-3n-4=0,解得n=-1(舍去)或n=4,
即袋中有4个黑球. …(4分)
(2)ξ可能的取值0,1,2,3,4.
∵ ,
,
P(ξ=1)=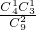 =
= ,
,
P(ξ=2)= =
=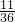 ,
,
 ,
,
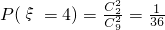 …(7分)
…(7分)
∴ξ的概率分布列为
 …(9分)
…(9分)
(3)记摸出的两个球中有一个红球为事件A,有一个黑球为事件B,则 为两个球都不是红球.
为两个球都不是红球.
所以两个球中有一个是红球的概率为 ,
,
两个球为一红一黑为事件A∩B,其概率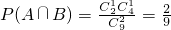 ,
,
所以在取得的两个球中有一个红球的条件下,另一个是黑球的概率为:
 .(12分)
.(12分)
分析:(1)由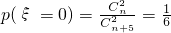 ,知n2-3n-4=0,由此能求出袋中有黑球个数.
,知n2-3n-4=0,由此能求出袋中有黑球个数.
(2)ξ可能的取值0,1,2,3,4. ,P(ξ=1)=
,P(ξ=1)=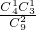 =
= ,P(ξ=2)=
,P(ξ=2)= =
=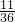 ,
, ,
,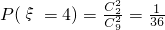 .由此能求出ξ的概率分布列和Eξ.
.由此能求出ξ的概率分布列和Eξ.
(3)记摸出的两个球中有一个红球为事件A,有一个黑球为事件B,则 为两个球都不是红球.所以两个球中有一个是红球的概率为
为两个球都不是红球.所以两个球中有一个是红球的概率为 ,两个球为一红一黑的概率
,两个球为一红一黑的概率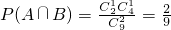 ,由此能求出取得的两个球中有一个红球的条件下,另一个是黑球的概率.
,由此能求出取得的两个球中有一个红球的条件下,另一个是黑球的概率.
点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意条件概率的性质和应用.
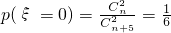 ,…(3分)
,…(3分)∴n2-3n-4=0,解得n=-1(舍去)或n=4,
即袋中有4个黑球. …(4分)
(2)ξ可能的取值0,1,2,3,4.
∵
 ,
,P(ξ=1)=
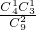 =
= ,
,P(ξ=2)=
 =
=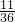 ,
, ,
,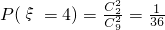 …(7分)
…(7分)∴ξ的概率分布列为
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |  |  | 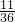 |  |  |
 …(9分)
…(9分)(3)记摸出的两个球中有一个红球为事件A,有一个黑球为事件B,则
 为两个球都不是红球.
为两个球都不是红球.所以两个球中有一个是红球的概率为
 ,
,两个球为一红一黑为事件A∩B,其概率
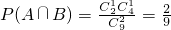 ,
,所以在取得的两个球中有一个红球的条件下,另一个是黑球的概率为:
 .(12分)
.(12分)分析:(1)由
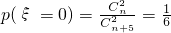 ,知n2-3n-4=0,由此能求出袋中有黑球个数.
,知n2-3n-4=0,由此能求出袋中有黑球个数.(2)ξ可能的取值0,1,2,3,4.
 ,P(ξ=1)=
,P(ξ=1)=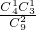 =
= ,P(ξ=2)=
,P(ξ=2)= =
=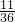 ,
, ,
,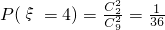 .由此能求出ξ的概率分布列和Eξ.
.由此能求出ξ的概率分布列和Eξ.(3)记摸出的两个球中有一个红球为事件A,有一个黑球为事件B,则
 为两个球都不是红球.所以两个球中有一个是红球的概率为
为两个球都不是红球.所以两个球中有一个是红球的概率为 ,两个球为一红一黑的概率
,两个球为一红一黑的概率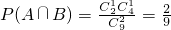 ,由此能求出取得的两个球中有一个红球的条件下,另一个是黑球的概率.
,由此能求出取得的两个球中有一个红球的条件下,另一个是黑球的概率.点评:本题考查离散型随机变量的分布列和数学期望,考查学生的运算能力,考查学生探究研究问题的能力,解题时要认真审题,注意条件概率的性质和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目