题目内容
(09 年聊城一模理) 已知在平面直角坐标系中,![]() ,动点
,动点![]() 满足条件
满足条件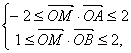 , 则
, 则![]() 的最大值为( )
的最大值为( )
A.-1 B.
答案:D

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
题目内容
(09 年聊城一模理) 已知在平面直角坐标系中,![]() ,动点
,动点![]() 满足条件
满足条件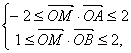 , 则
, 则![]() 的最大值为( )
的最大值为( )
A.-1 B.

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案