题目内容
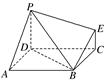
右图为一简单组合体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝AD＝2EC＝2.
(1)请画出该几何体的三视图；
(2)求四棱锥BCEPD的体积．
(1)请画出该几何体的三视图；
(2)求四棱锥BCEPD的体积．
(1)见解析 (2)2
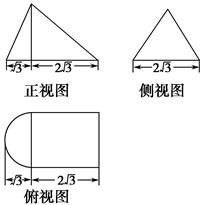
解：(1)该组合体的三视图如图所示．
(2)∵PD⊥平面ABCD，
PD?平面PDCE，
∴平面PDCE⊥平面ABCD.
∵四边形ABCD为正方形，
∴BC⊥CD，且BC＝DC＝AD＝2.
又∵平面PDCE∩平面ABCD＝CD，
BC?平面ABCD.
∴BC⊥平面PDCE.
∵PD⊥平面ABCD，DC?平面ABCD，
∴PD⊥DC.
又∵EC∥PD，PD＝2，EC＝1，
∴四边形PDCE为一个直角梯形，其面积：
S梯形PDCE＝
(PD＋EC)·DC＝×3×2＝3，
∴四棱锥BCEPD的体积
VBCEPD＝
S梯形PDCE·BC＝×3×2＝2.
(2)∵PD⊥平面ABCD，
PD?平面PDCE，
∴平面PDCE⊥平面ABCD.
∵四边形ABCD为正方形，
∴BC⊥CD，且BC＝DC＝AD＝2.
又∵平面PDCE∩平面ABCD＝CD，
BC?平面ABCD.
∴BC⊥平面PDCE.
∵PD⊥平面ABCD，DC?平面ABCD，
∴PD⊥DC.
又∵EC∥PD，PD＝2，EC＝1，
∴四边形PDCE为一个直角梯形，其面积：
S梯形PDCE＝
(PD＋EC)·DC＝×3×2＝3，∴四棱锥BCEPD的体积
VBCEPD＝
S梯形PDCE·BC＝×3×2＝2.
练习册系列答案
相关题目
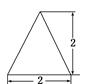
的正方形ABCD沿对角线BD折起，连结AC，得到三棱锥C-ABD，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为( )
，8
)cm2
