题目内容
把100个面包分给5个人,使每人所得的面包数成等差数列,且使较多的三份之和的 等于较少的两份之和,则最少的一份面包个数是________.
等于较少的两份之和,则最少的一份面包个数是________.
10
分析:设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,则由题意可得 ,解得a和d的值,即可得到最少的一份为a-2d的值.
,解得a和d的值,即可得到最少的一份为a-2d的值.
解答:设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,
则由题意可得 ,解得
,解得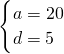 ,
,
则最少的一份为a-2d=10.
答案:10
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式的应用,设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,是解题的突破口,属于基础题.
分析:设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,则由题意可得
 ,解得a和d的值,即可得到最少的一份为a-2d的值.
,解得a和d的值,即可得到最少的一份为a-2d的值.解答:设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,
则由题意可得
 ,解得
,解得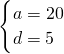 ,
,则最少的一份为a-2d=10.
答案:10
点评:本题主要考查等差数列的定义和性质,等差数列的通项公式的应用,设构成等差数列的五个数为a-2d,a-d,a,a+d,a+2d,是解题的突破口,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
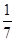 是较小的两份之和,问最小1份是( )
是较小的两份之和,问最小1份是( )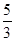 B.
B.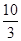 C.
C.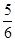 D.
D.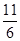
 是较小的两份之和,则最小1份是( )
是较小的两份之和,则最小1份是( )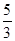 B.
B. C.
C.  D.
D. 