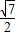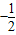题目内容
已知角A为△ABC的内角,且sin2A=-
,则sinA-cosA=( )
| 3 |
| 4 |
分析:由角A为△ABC的内角,sin2A=-
可知∠A为钝角,从而sinA>0,-cosA>0,sinA-cosA>0,于是先(sinA-cosA)2,
再开方即可.
| 3 |
| 4 |
再开方即可.
解答:解:角A为△ABC的内角,
∴sinA>0,
∵sin2A=-
,而sin2A=2sinAcosA,
∴cosa<0,
∴∠A为钝角,
∴sinA-cosA>0,
∴(sinA-cosA)2=1-sin2A=1+
=
,
∴sinA-cosA=
.
故选A.
∴sinA>0,
∵sin2A=-
| 3 |
| 4 |
∴cosa<0,
∴∠A为钝角,
∴sinA-cosA>0,
∴(sinA-cosA)2=1-sin2A=1+
| 3 |
| 4 |
| 7 |
| 4 |
∴sinA-cosA=
| ||
| 2 |
故选A.
点评:本题考查同角三角函数间的基本关系,着重考察正弦函数的二倍角公式的应用,难点在于sinA-cosA符号的判断,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
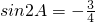 ,则sinA-cosA=
,则sinA-cosA=
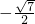


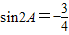 ,则sinA-cosA=( )
,则sinA-cosA=( )