题目内容
在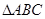 中,角A、B、C所对的边分别为a,b,c,S表示
中,角A、B、C所对的边分别为a,b,c,S表示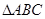 的面积,若
的面积,若 =
=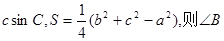 ( )
( )
| A.90° | B.60° | C.45° | D.30° |
C
解析考点:正弦定理;两角和与差的正弦函数;余弦定理的应用.
分析:先利用正弦定理把acosB+bcosA=csinC中的边换成角的正弦,利用两角和公式化简整理可求得C=90°,进而可利用两直角边表示出三角形的面积,利用勾股定理化简整理可求得a=b,推断出三角形为直角等腰三角形,进而求得B.
解:由正弦定理可知a=2rsinA,b=2rsinB,c=2rsinC,
∵acosB+bcosA=csinC,
∴sinAcosB+sinBcosA=sinCsinC,即sin(A+B)=sin2C,
∵A+B=π-c
∴sin(A+B)=sinC=sin2C,
∵0<C<π
∴sinC≠0
∴sinC=1
∴C=90°
∴S=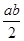 =
=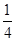 (b2+c2-a2)
(b2+c2-a2)
∵b2+a2=c2,
∴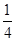 (b2+c2-a2)=
(b2+c2-a2)=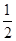 b2=
b2=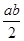
∴a=b
∴△ABC为等腰直角三角形
∴∠B=45°
故答案为C

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是  ,且
,且 =2,
=2,
 .
. 的值.
的值. =3,求b,c的值.
=3,求b,c的值.  中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知 ,
, ,则
,则 = _______
= _______ (
( ,
, ),且函数
),且函数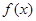 的最小正周期为
的最小正周期为 .
. 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 ,若
,若 =1,
=1,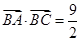 ,且
,且 ,求边长
,求边长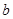 .
. 中,角A,B,C所对的边分别为a,b,c,若
中,角A,B,C所对的边分别为a,b,c,若 ,
, ,
, ,则角A的大小为
,则角A的大小为  中,角A、B、C所对的边分别为a,b,c,S表示
中,角A、B、C所对的边分别为a,b,c,S表示 =
= ( )
( )