题目内容
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱BC的中点.(Ⅰ)求证:AD⊥平面BCC1B1;
(Ⅱ)求证:A1B∥平面AC1D;
(Ⅲ)求平面AC1D与平面ACC1A1所成的锐二面角的余弦值.

【答案】分析:(Ⅰ)先证明AA1⊥平面ABC,可得CC1⊥AD,再利用线面垂直的判定定理,即可证明AD⊥平面BCC1B1;
(Ⅱ)利用三角形中位线的性质,证明A1B∥OD,利用线面平行的判定定理证明A1B∥平面AC1D;
(Ⅲ)建立空间直角坐标系,求出平面AC1D与平面ACC1A1的法向量,利用向量的夹角公式,即可求锐二面角的余弦值.
解答:(Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形
所以AA1⊥AC,AA1⊥AB
所以AA1⊥平面ABC …(1分)
因为AD?平面ABC,AA1∥CC1,所以CC1⊥AD …(2分)
又因为AB=AC,D为BC中点,所以AD⊥BC …(3分)
因为CC1∩BC=C,所以AD⊥平面BCC1B1; …(4分)
(Ⅱ)证明:连结A1C,交AC1于点O,连结OD
因为ACC1A1为正方形,所以O为AC1中点
又D为BC中点,所以OD为△A1BC中位线
所以A1B∥OD …(6分)
因为OD?平面AC1D,AB1?平面AC1D
所以A1B∥平面AC1D…(8分)
(Ⅲ)解:因为侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°
所以AB,AC,AA1两两互相垂直,如图所示建立直角坐标系A-xyz
设AB=1,则A(0,0,0),
∴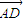 =
= ,
,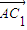 =(0,1,1)…(9分)
=(0,1,1)…(9分)
设平面AC1D的法向量为 =(x,y,z),则有
=(x,y,z),则有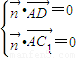 ,
,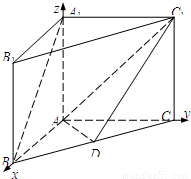
∴ ,∴x=-y=z
,∴x=-y=z
取x=1,得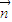 =(1,-1,1)…(10分)
=(1,-1,1)…(10分)
又因为AB⊥平面ACC1A1
所以平面ACC1A1的法向量为 …(11分)
…(11分)
∴cos< >=
>=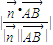 =
= =
=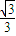 …(12分)
…(12分)
所以,平面AC1D与平面ACC1A1所成的锐二面角的余弦值为 …(13分)
…(13分)
点评:本题考查线面垂直,线面平行,考查面面角,考查空间向量知识的运用,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)利用三角形中位线的性质,证明A1B∥OD,利用线面平行的判定定理证明A1B∥平面AC1D;
(Ⅲ)建立空间直角坐标系,求出平面AC1D与平面ACC1A1的法向量,利用向量的夹角公式,即可求锐二面角的余弦值.
解答:(Ⅰ)证明:因为侧面ABB1A1,ACC1A1均为正方形
所以AA1⊥AC,AA1⊥AB
所以AA1⊥平面ABC …(1分)
因为AD?平面ABC,AA1∥CC1,所以CC1⊥AD …(2分)
又因为AB=AC,D为BC中点,所以AD⊥BC …(3分)
因为CC1∩BC=C,所以AD⊥平面BCC1B1; …(4分)
(Ⅱ)证明:连结A1C,交AC1于点O,连结OD

因为ACC1A1为正方形,所以O为AC1中点
又D为BC中点,所以OD为△A1BC中位线
所以A1B∥OD …(6分)
因为OD?平面AC1D,AB1?平面AC1D
所以A1B∥平面AC1D…(8分)
(Ⅲ)解:因为侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°
所以AB,AC,AA1两两互相垂直,如图所示建立直角坐标系A-xyz
设AB=1,则A(0,0,0),

∴
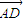 =
= ,
,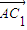 =(0,1,1)…(9分)
=(0,1,1)…(9分)设平面AC1D的法向量为
 =(x,y,z),则有
=(x,y,z),则有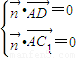 ,
,
∴
 ,∴x=-y=z
,∴x=-y=z取x=1,得
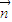 =(1,-1,1)…(10分)
=(1,-1,1)…(10分)又因为AB⊥平面ACC1A1
所以平面ACC1A1的法向量为
 …(11分)
…(11分)∴cos<
 >=
>=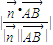 =
= =
=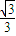 …(12分)
…(12分)所以,平面AC1D与平面ACC1A1所成的锐二面角的余弦值为
 …(13分)
…(13分)点评:本题考查线面垂直,线面平行,考查面面角,考查空间向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=