题目内容
已知函数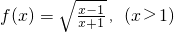
(1)求函数f(x)的反函数 f-1(x)及其定义域;
(2)若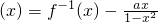 在区间
在区间 上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
解:(1)设y= ,
,
则 ,y>0,
,y>0,
 ,
,
x,y互换,得 .
.
∵y= ,
,
∴y>0,
∴f-1(x)= ,其定义域为{x|x>0}.
,其定义域为{x|x>0}.
(2)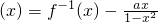
=
= ,
,
∵m=1-x2在区间 上是单调减函数,∅(x)=
上是单调减函数,∅(x)= 在区间
在区间 上是单调增函数,
上是单调增函数,
∴n=x2-ax+1在区间 上是单调增函数,
上是单调增函数,
∴ ,
,
∴a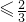 .
.
分析:(1)设y= ,则
,则 ,y>0,由此能求出f-1(x)和其定义域.
,y>0,由此能求出f-1(x)和其定义域.
(2)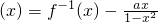 =
= ,由m=1-x2在区间
,由m=1-x2在区间 上是单调减函数,∅(x)=
上是单调减函数,∅(x)= 在区间
在区间 上是单调增函数,知n=x2-ax+1在区间
上是单调增函数,知n=x2-ax+1在区间 上是单调增函数,由此能求出实数a的取值范围.
上是单调增函数,由此能求出实数a的取值范围.
点评:本题考查反函数的求法和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 ,
,则
 ,y>0,
,y>0, ,
,x,y互换,得
 .
.∵y=
 ,
,∴y>0,
∴f-1(x)=
 ,其定义域为{x|x>0}.
,其定义域为{x|x>0}.(2)
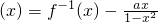
=

=
 ,
,∵m=1-x2在区间
 上是单调减函数,∅(x)=
上是单调减函数,∅(x)= 在区间
在区间 上是单调增函数,
上是单调增函数,∴n=x2-ax+1在区间
 上是单调增函数,
上是单调增函数,∴
 ,
,∴a
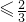 .
.分析:(1)设y=
 ,则
,则 ,y>0,由此能求出f-1(x)和其定义域.
,y>0,由此能求出f-1(x)和其定义域.(2)
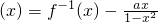 =
= ,由m=1-x2在区间
,由m=1-x2在区间 上是单调减函数,∅(x)=
上是单调减函数,∅(x)= 在区间
在区间 上是单调增函数,知n=x2-ax+1在区间
上是单调增函数,知n=x2-ax+1在区间 上是单调增函数,由此能求出实数a的取值范围.
上是单调增函数,由此能求出实数a的取值范围.点评:本题考查反函数的求法和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线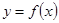 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)