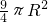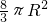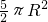题目内容
已知向量 ,且
,且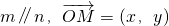 (O为坐标原点).
(O为坐标原点).
(1)求点M的轨迹C的方程;
(2)是否存在过点F(1,0)的直线l与曲线C相 交于A、B两点,并且曲线C存在点P,使四边形OAPB为平行四边形?若存在,求出平行四边形OAPB的面积;若不存在,说明理由.
解:(1)∵向量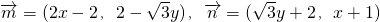 ,且
,且
∴(2x-2)(x+1)-(2-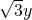 )
) =0
=0
化简可得,点M的轨迹C的方程为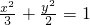 ;
;
(2)设A(x1,y1),B(x2,y2),
由题意知l的斜率一定不为0,故不妨设l:x=my+1,代入椭圆方程,消元可得(2m2+3)y2+4my-4=0
∴y1+y2=- ,y1y2=-
,y1y2=-
假设存在点P,使四边形OAPB为平行四边形,其充要条件为
∴P(x1+x2,y1+y2)
∴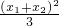 +
+ =1
=1
∴2 +3
+3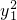 +2
+2 +3
+3 +4x1x2+6y1y2=6
+4x1x2+6y1y2=6
∵A,B在椭圆上,∴2 +3
+3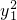 =6,2
=6,2 +3
+3 ,=6
,=6
∴2x1x2+3y1y2=-3
∵y1+y2=- ,y1y2=-
,y1y2=-
∴m=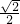
当m= 时,y1=
时,y1= ,y2=
,y2= ,∴x1=0,x2=
,∴x1=0,x2=
∴
∴cos
∴sin∠AOB=
∴平行四边形OAPB的面积为
当m=- 时,同理可得平行四边形OAPB的面积为
时,同理可得平行四边形OAPB的面积为
故存在存在点P,使四边形OAPB为平行四边形.
分析:(1)利用向量共线的条件,建立方程,化简可得点M的轨迹C的方程;
(2)设A(x1,y1),B(x2,y2),设l:x=my+1,代入椭圆方程,消元可得(2m2+3)y2+4my-4=0,利用韦达定理表示,假设存在点P,使四边形OAPB为平行四边形,其充要条件为 ,从而可得P的坐标,代入椭圆方程,利用A,B在椭圆上,可求m的值,进而可求平行四边形OAPB的面积,即可得到结论.
,从而可得P的坐标,代入椭圆方程,利用A,B在椭圆上,可求m的值,进而可求平行四边形OAPB的面积,即可得到结论.
点评:本题考查轨迹方程,考查向量知识的运用,考查直线与椭圆的位置关系,考查三角形面积的计算,确定直线的方程是关键.
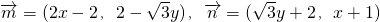 ,且
,且
∴(2x-2)(x+1)-(2-
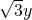 )
) =0
=0化简可得,点M的轨迹C的方程为
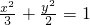 ;
;(2)设A(x1,y1),B(x2,y2),
由题意知l的斜率一定不为0,故不妨设l:x=my+1,代入椭圆方程,消元可得(2m2+3)y2+4my-4=0
∴y1+y2=-
 ,y1y2=-
,y1y2=-
假设存在点P,使四边形OAPB为平行四边形,其充要条件为

∴P(x1+x2,y1+y2)
∴
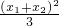 +
+ =1
=1∴2
 +3
+3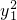 +2
+2 +3
+3 +4x1x2+6y1y2=6
+4x1x2+6y1y2=6∵A,B在椭圆上,∴2
 +3
+3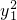 =6,2
=6,2 +3
+3 ,=6
,=6∴2x1x2+3y1y2=-3
∵y1+y2=-
 ,y1y2=-
,y1y2=-
∴m=
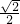
当m=
 时,y1=
时,y1= ,y2=
,y2= ,∴x1=0,x2=
,∴x1=0,x2=
∴

∴cos

∴sin∠AOB=

∴平行四边形OAPB的面积为

当m=-
 时,同理可得平行四边形OAPB的面积为
时,同理可得平行四边形OAPB的面积为
故存在存在点P,使四边形OAPB为平行四边形.
分析:(1)利用向量共线的条件,建立方程,化简可得点M的轨迹C的方程;
(2)设A(x1,y1),B(x2,y2),设l:x=my+1,代入椭圆方程,消元可得(2m2+3)y2+4my-4=0,利用韦达定理表示,假设存在点P,使四边形OAPB为平行四边形,其充要条件为
 ,从而可得P的坐标,代入椭圆方程,利用A,B在椭圆上,可求m的值,进而可求平行四边形OAPB的面积,即可得到结论.
,从而可得P的坐标,代入椭圆方程,利用A,B在椭圆上,可求m的值,进而可求平行四边形OAPB的面积,即可得到结论.点评:本题考查轨迹方程,考查向量知识的运用,考查直线与椭圆的位置关系,考查三角形面积的计算,确定直线的方程是关键.

练习册系列答案
相关题目
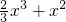 +ax+b(x>-1).
+ax+b(x>-1).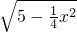 只有一个公共点,则m的取值范围是
只有一个公共点,则m的取值范围是 ≤m≤2
≤m≤2
 ,则下列关系中正确的是
,则下列关系中正确的是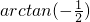
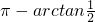

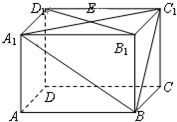 如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=1,E是A1C1与B1D1的交点.
如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,AA1=1,E是A1C1与B1D1的交点. =1有相同的渐近线,且过点(4,4)的双曲线.
=1有相同的渐近线,且过点(4,4)的双曲线. ,该圆柱的全面积为
,该圆柱的全面积为