题目内容
某校研究性学习小组利用假期时间从年龄在[25，55]内的人群中随机抽取n人，进行是否具有终身学习观念的调查，得到如下统计表和各年龄段人数频率分布直方图：
| 组别 | 年龄段 | 具有终身学习观念的人数 |  |
| 第一组 | [25，30） | 120 | 0.6 |
| 第二组 | [30，35） | 195 | 0.65 |
| 第三组 | [35，40） | 100 | p |
| 第四组 | [40，45） | 60 | 0.4 |
| 第五组 | [45，50） | a | 0.3 |
| 第六组 | [50，55] | 15 | 0.3 |
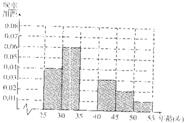
（II）从年龄在[40，50）内且具有终身学习观念的人中采用分层抽样法抽取12人参加某项学习活动，从这12名中再选取3人作为领队，记这3名领队中年龄在[40，50）内的人数为X，求X的分布列和期望EX．
解：（I）第三小组的频率为1-（0.04+0.06+0.03+0.02+0.01）×5=0.2∴小矩形的高为0.04，频率分步直方图如下：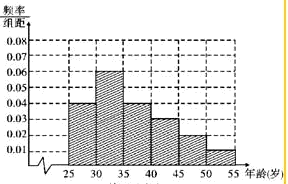
第一组的人数为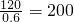
，
频率为0.04×5=0.2
∴n=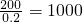
∴p=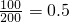
，a=100×0.3=30
（II）∵[40，45）年龄段的具有终身学习观念的人中采用分层抽样法抽取12人参加某项学习活动，
[40，45）年龄段要抽8人，[45，50）要抽4人，
随机变量X的可能取值是0，1，2，3
P（X=3）=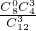
=
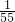，P（X=2）=
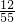，P（X=，1）=
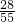，P（X=0）=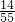
∴X的分布列是
∴EX=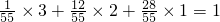
分析：（I）根据所给的除去第三小组以外的小矩形的长与宽，得到第三小组的频率．进而得到矩形高，画出频率分步直方图．根据频数，频率和样本容量之间的关系做出字母的值．
（II）由题意知变量的可能取值，结合变量对应的事件，写出变量的概率，写出分布列和期望值．
点评：本题考查离散型随机变量的分布列和期望，本题解题的关键是正确使用频率分步直方图，从图形中能够找到要用的条件．
第一组的人数为
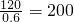，频率为0.04×5=0.2
∴n=
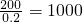
∴p=
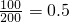，a=100×0.3=30（II）∵[40，45）年龄段的具有终身学习观念的人中采用分层抽样法抽取12人参加某项学习活动，
[40，45）年龄段要抽8人，[45，50）要抽4人，
随机变量X的可能取值是0，1，2，3
P（X=3）=
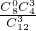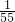=，P（X=2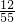）=，P（X=，1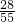）=，P（X=0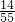）=∴X的分布列是
| X | 3 | 2 | 1 | 0 |
| P | | | | |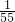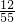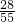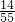
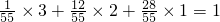
分析：（I）根据所给的除去第三小组以外的小矩形的长与宽，得到第三小组的频率．进而得到矩形高，画出频率分步直方图．根据频数，频率和样本容量之间的关系做出字母的值．
（II）由题意知变量的可能取值，结合变量对应的事件，写出变量的概率，写出分布列和期望值．
点评：本题考查离散型随机变量的分布列和期望，本题解题的关键是正确使用频率分步直方图，从图形中能够找到要用的条件．
练习册系列答案
相关题目
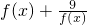的最小值及对应的x值．
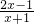（x≠-1）的反函数是f-1（x），则f-1（0）=
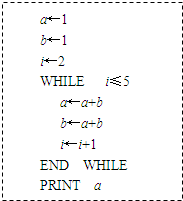下列程序运算后的结果是________．
上的一点到其左、右焦点的距离之差为4，若已知抛物线y=ax2上的两点A（x1，y1），B（x2，y2）关于直线y=x+m对称，且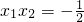
，则m的值为
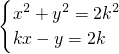仅有一组实数解，则符合条件的实数k的个数是