题目内容
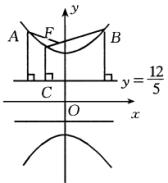
在双曲线![]() =-1的一支上有不同三点A(x1,y1)、B(x2,6)、C(x3,y3)与点F(0,5)的距离|AF|、|BF|、|CF|依次成等差数列。
=-1的一支上有不同三点A(x1,y1)、B(x2,6)、C(x3,y3)与点F(0,5)的距离|AF|、|BF|、|CF|依次成等差数列。
(1)求y1+y3的值;
(2)求证线段AC的垂直平分线经过某一定点,并求出定点的坐标。
答案:
解析:
解析:
双曲线的标准方程 (1)a2=12,b2=13,∵c2=25,
∵2|BF|=|AF|+|CF|,∴y1+y3=12. (也可以用第一定义求解,请读者自己完成)。 (2)设AC的中点为M(x0,y0),则y0= ∵A、C在双曲线上,
①—②,得 ∴ ∴ ∴ AC的垂直平分线的方程是y-6=
|

练习册系列答案
相关题目
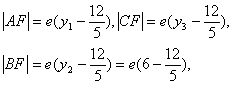
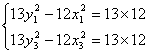
 如图,在双曲线
如图,在双曲线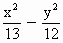 =-1的一支上有不同三点A
=-1的一支上有不同三点A ,6),C(
,6),C( )与焦点F(0,5)的距离成等差数列,(1)求
)与焦点F(0,5)的距离成等差数列,(1)求 ;(2)求证线段AC的垂直平分线经过某一定点,并求出定点的坐标.
;(2)求证线段AC的垂直平分线经过某一定点,并求出定点的坐标.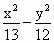 =-1的一支上有不同的三点A(
=-1的一支上有不同的三点A( ,
, ),B(
),B( ,6),C(
,6),C( ,
, )与焦点F(0,5)的距离成等差数列.
)与焦点F(0,5)的距离成等差数列.