题目内容
估计总体的数字特征过程中,我们经常用到样本均值与样本标准差,这两个有什么差别吗?
解析:
|
探究过程:学生甲:我认为它们两个在表达式上就不同,假设经过随机抽样得到样本为x1、x2,…,xn, 则样本均值 样本标准差s= 学生乙:我看出来它们还有一些不同的地方,先来看下面的例子. (1)有两个学生A和B,两个人两次连续考试的平均分都是60分,A是40分和80分,B是65分和55分.显然A的成绩忽上忽下,而B的成绩较稳定. (2)有两组学生(每组3人),一次数学考试成绩如下(单位:分): 甲组3人得分分别为60 80 100 乙组3人得分分别为79 80 81 显然,甲组学生和乙组学生的平均分都为80,但是这两组学生分数有很大的差异,甲组学生的成绩波动较大,相对于平均分数的差异很大,即分散程度(离中趋势)较大,而乙组学生的成绩波动较小,相对于平均分数的差异较小,即分散程度较小.因此,我们仅用平均值来描述这一组分数的特征是不够的,还要考虑一组分数相对于平均值的差异的大小.在考试研究中,均值反应了考生团体成绩集中的位置,根据以上分析,显然还需有一个刻画考生团体成绩离散程度的量,显然在刚才举的例子(1)中, sA= 在(2)中, 乙组学生的s乙= 探究结论:明显地发现样本平均数能反映总体的水平,而标准差对于衡量分散程度很有用. |

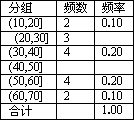
一个容量为M的样本数据,其频率分布表如下.
(Ⅰ)完成频率分布表 ;
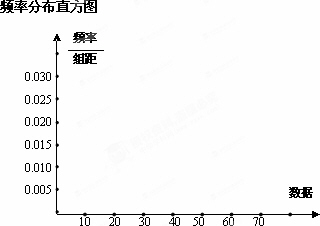
(Ⅱ)画出频率分布直方图 ;
(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数.
 【解】 频率分布表 频率分布直方图
【解】 频率分布表 频率分布直方图
|
分组 |
频数 |
频率 |
|
(10,20] |
2 |
0.10 |
|
(20,30] |
3 |
|
|
(30,40] |
4 |
0.20 |
|
(40,50] |
|
|
|
(50,60] |
4 |
0.20 |
|
(60,70] |
2 |
0.10 |
|
合计 |
|
1.00 |