题目内容
2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏,某国际组织计划派出12名心理专家和18名核专家赴日本工作,临行前对这30名专家进行了总分为1000分的综合素质测评,测评成绩用茎叶图进行了记录,如图(单位:分).规定测评成绩在976分以上(包括976)为“尖端专家”,测评成绩在976分以下为“高级专家”,且只有核专家中的“尖端专家”才可以独立开展工作,这些专家先飞抵日本的城市E,再分乘三辆汽车到达工作地点福岛县.已知从城市E到福岛县有三条公路,因地震破坏了道路,汽车可能受阻.据了解:汽车走公路I和公路II顺利到达的概率都为 ;走公路III顺利到达的概率为
;走公路III顺利到达的概率为 ,甲、乙、丙三辆车分别走公路I、II、III,且三辆汽车是否顺利到达相互之间没有影响.
,甲、乙、丙三辆车分别走公路I、II、III,且三辆汽车是否顺利到达相互之间没有影响.(I)如果用分层抽样的方法从“尖端专家”和“高级专家”中选取6人,再从这6人中选2人,那么至少有一人是“尖端专家”的概率是多少?
(Ⅱ)求至少有两辆汽车顺利到达福岛县的概率;
(Ⅲ)若从所有“尖端专家”中选3名志愿者,用ξ表示所选志愿者中能独立开展工作的人数,试写出ξ的数学期望.

【答案】分析:(I)根据茎叶图和由分层抽样的特点可知6人中“尖端专家”2人,“高级专家”4人,可得P=1-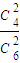 ,计算可得;
,计算可得;
(Ⅱ)记“汽车从公路I顺利到达”为事件A,“汽车从公路II顺利到达”为事件B,“汽车从公路III顺利到达”为事件C,则P=P(AB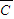 )+P(A
)+P(A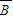 C)+P(
C)+P(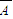 BC)+P(ABC),由独立事件的概率计算可得;(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,可得ξ的取值为0,1,2,3,分别求概率可得分布列,可得期望.
BC)+P(ABC),由独立事件的概率计算可得;(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,可得ξ的取值为0,1,2,3,分别求概率可得分布列,可得期望.
解答:解:(I)根据茎叶图可知,有“尖端专家”10人,“高级专家”20人,
每个人被抽到的概率是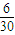 =
=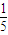 ,
,
由分层抽样可知选出的“尖端专家”10×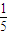 =2人,“高级专家”20×
=2人,“高级专家”20×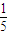 =4人,
=4人,
用事件A表示至少有一名“尖端专家”被选中,则P(A)=1-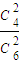 =1-
=1-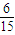 =
=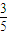
故至少有一人是“尖端专家”的概率是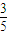
(Ⅱ)记“汽车从公路I顺利到达”为事件A,“汽车从公路II顺利到达”为事件B,
“汽车从公路III顺利到达”为事件C,则至少有两辆汽车顺利到达福岛县的概率为
P=P(AB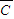 )+P(A
)+P(A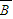 C)+P(
C)+P(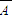 BC)+P(ABC)
BC)+P(ABC)
=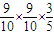 +
+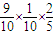 +
+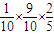 +
+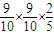 =
=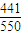 ;
;
(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,
依题意可得ξ的取值为0,1,2,3,P(ξ=0)= =
=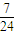 ,P(ξ=1)=
,P(ξ=1)=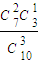 =
=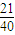 ,
,
P(ξ=2)=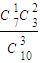 =
=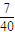 ,P(ξ=3)=
,P(ξ=3)=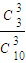 =
=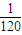 ,
,
故可得分布列如下:
故ξ的数学期望Eξ=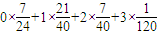 =
=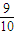
点评:本题考查离散型随机变量的期望,涉及茎叶图和独立事件的概率公式,属中档题.
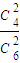 ,计算可得;
,计算可得;(Ⅱ)记“汽车从公路I顺利到达”为事件A,“汽车从公路II顺利到达”为事件B,“汽车从公路III顺利到达”为事件C,则P=P(AB
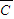 )+P(A
)+P(A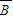 C)+P(
C)+P(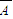 BC)+P(ABC),由独立事件的概率计算可得;(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,可得ξ的取值为0,1,2,3,分别求概率可得分布列,可得期望.
BC)+P(ABC),由独立事件的概率计算可得;(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,可得ξ的取值为0,1,2,3,分别求概率可得分布列,可得期望.解答:解:(I)根据茎叶图可知,有“尖端专家”10人,“高级专家”20人,
每个人被抽到的概率是
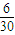 =
=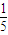 ,
,由分层抽样可知选出的“尖端专家”10×
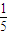 =2人,“高级专家”20×
=2人,“高级专家”20×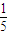 =4人,
=4人,用事件A表示至少有一名“尖端专家”被选中,则P(A)=1-
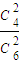 =1-
=1-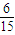 =
=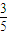
故至少有一人是“尖端专家”的概率是
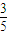
(Ⅱ)记“汽车从公路I顺利到达”为事件A,“汽车从公路II顺利到达”为事件B,
“汽车从公路III顺利到达”为事件C,则至少有两辆汽车顺利到达福岛县的概率为
P=P(AB
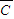 )+P(A
)+P(A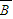 C)+P(
C)+P(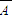 BC)+P(ABC)
BC)+P(ABC)=
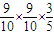 +
+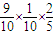 +
+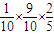 +
+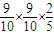 =
=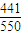 ;
;(Ⅲ)由茎叶图可知,心理专家中的“尖端专家”为7人,核专家中的“尖端专家”为3人,
依题意可得ξ的取值为0,1,2,3,P(ξ=0)=
 =
=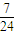 ,P(ξ=1)=
,P(ξ=1)=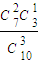 =
=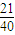 ,
,P(ξ=2)=
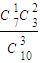 =
=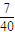 ,P(ξ=3)=
,P(ξ=3)=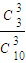 =
=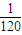 ,
,故可得分布列如下:
| ξ | 0 | 1 | 2 | 3 |
| P | 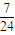 | 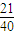 | 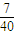 | 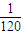 |
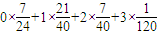 =
=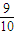
点评:本题考查离散型随机变量的期望,涉及茎叶图和独立事件的概率公式,属中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏.某国际组织用分层抽样的方法从心理专家、核专家、地质专家三类专家中抽取若干人组成研究小组赴日本工作,有关数据见表1(单位:人).
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
附:临界值表
参考公式: ;
;
(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
| 相关人员数 | 抽取人数 | |
| 心理专家 | 24 | x |
| 核专家 | 48 | y |
| 地质专家 | 72 | 6 |
| 高度辐射 | 轻微辐射 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 ;
;(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏.某国际组织用分层抽样的方法从心理专家、核专家、地质专家三类专家中抽取若干人组成研究小组赴日本工作,有关数据见表1(单位:人).
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
附:临界值表
参考公式: ;
;
(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
| 相关人员数 | 抽取人数 | |
| 心理专家 | 24 | x |
| 核专家 | 48 | y |
| 地质专家 | 72 | 6 |
| 高度辐射 | 轻微辐射 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 ;
;(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏.某国际组织用分层抽样的方法从心理专家、核专家、地质专家三类专家中抽取若干人组成研究小组赴日本工作,有关数据见表1(单位:人).
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
附:临界值表
参考公式: ;
;
(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
核专家为了检测当地动物受核辐射后对身体健康的影响,随机选取了110只羊进行了检测,并将有关数据整理为不完整的2×2列联表(表2).
| 相关人员数 | 抽取人数 | |
| 心理专家 | 24 | x |
| 核专家 | 48 | y |
| 地质专家 | 72 | 6 |
| 高度辐射 | 轻微辐射 | 合计 | |
| 身体健康 | 30 | A | 50 |
| 身体不健康 | B | 10 | 60 |
| 合计 | C | D | E |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 ;
;(1)求研究小组的总人数;
(2)写出表2中A、B、C、D、E的值,并判断有多大的把握认为羊受到高度辐射与身体不健康有关;
(3)若从研究小组的心理专家和核专家中随机选2人撰写研究报告,求其中恰好有1人为心理专家的概率.
 (2011•潍坊二模)2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏,某国际组织计划派出12名心理专家和18名核专家赴日本工作,临行前对这30名专家进行了总分为1000分的综合素质测评,测评成绩用茎叶图进行了记录,如图(单位:分).规定测评成绩在976分以上(包括976)为“尖端专家”,测评成绩在976分以下为“高级专家”,且只有核专家中的“尖端专家”才可以独立开展工作,这些专家先飞抵日本的城市E,再分乘三辆汽车到达工作地点福岛县.已知从城市E到福岛县有三条公路,因地震破坏了道路,汽车可能受阻.据了解:汽车走公路I和公路II顺利到达的概率都为
(2011•潍坊二模)2011年3月,日本发生了9.0级地震,地震引发了海啸及核泄漏,某国际组织计划派出12名心理专家和18名核专家赴日本工作,临行前对这30名专家进行了总分为1000分的综合素质测评,测评成绩用茎叶图进行了记录,如图(单位:分).规定测评成绩在976分以上(包括976)为“尖端专家”,测评成绩在976分以下为“高级专家”,且只有核专家中的“尖端专家”才可以独立开展工作,这些专家先飞抵日本的城市E,再分乘三辆汽车到达工作地点福岛县.已知从城市E到福岛县有三条公路,因地震破坏了道路,汽车可能受阻.据了解:汽车走公路I和公路II顺利到达的概率都为