题目内容
若a为实数，则圆（x-a）2+（y+2a）2=1的圆心所在的直线方程为
- A.2x+y=0
- B.x+2y=0
- C.x-2y=0
- D.2x-y=0
A
分析：由题意求出圆心坐标，再消去a可得到圆心所在的直线方程．
解答：由题意知，圆心坐标为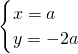
，
消去a得，2x+y=0；
故圆心所在的直线方程为2x+y=0，
故选A．
点评：本题考查了圆的标准方程和参数法求直线方程，这是求轨迹方程常用的一种方法．
分析：由题意求出圆心坐标，再消去a可得到圆心所在的直线方程．
解答：由题意知，圆心坐标为
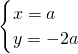，消去a得，2x+y=0；
故圆心所在的直线方程为2x+y=0，
故选A．
点评：本题考查了圆的标准方程和参数法求直线方程，这是求轨迹方程常用的一种方法．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
若a为实数，则圆（x-a）2+（y+2a）2=1的圆心所在的直线方程为（ ）
| A、2x+y=0 | B、x+2y=0 | C、x-2y=0 | D、2x-y=0 |