题目内容
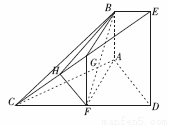
(本小题12分)如图,已知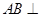 平面
平面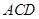 ,
,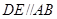 ,
,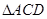 为等边三角形,
为等边三角形,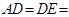
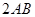 ,
,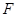 为
为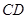 的中点.
的中点.
(1)求证: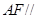 平面
平面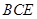 ;
;
(2)求证:平面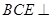 平面
平面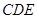 ;
;
(3)求直线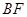 和平面
和平面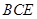 所成角的正弦值.
所成角的正弦值.

【答案】
(1)证明:见解析;(2)见解析.(3)直线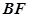 和平面
和平面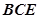 所成角的正弦值为
所成角的正弦值为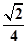 .
.
【解析】(1)解本题的关键是在平面BEC内构造出一条与AF平行的平行线。取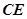 的中点
的中点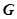 ,连
,连 、
、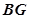 ,然后证明四边形BGFA为平行四边形即可。
,然后证明四边形BGFA为平行四边形即可。
(2) 关键是证: 平面
平面 ,即证:
,即证: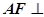 平面
平面 ,即CD的中点F,即证:
,即CD的中点F,即证: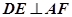 和
和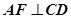 即可。
即可。
(3)解本小题的关键是找出线面角。在平面 内,过
内,过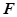 作
作 于
于 ,连
,连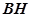
∵平面 平面
平面 ,∴
,∴ 平面
平面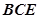 ,
,
∴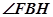 为
为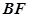 和平面
和平面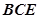 所成的角。然后解三角形即可。
所成的角。然后解三角形即可。
(1)证明:取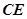 的中点
的中点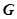 ,连
,连 、
、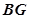 .
.
∵ 为
为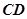 的中点,∴
的中点,∴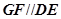 且
且
∵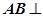 平面
平面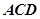 ,
,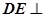 平面
平面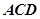 .
.
∴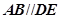 ,∴
,∴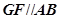
又 ,∴
,∴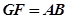
∴四边形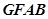 为平行四边形,因此
为平行四边形,因此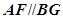
∵ 平面
平面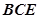 ,
, 平面
平面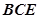 .
.
∴ 平面
平面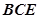 …………………………………4分
…………………………………4分
(2)证明:∵ 是等边三角形,
是等边三角形,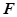 为
为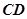 的中点,
的中点,
∴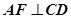 ∵
∵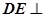 平面
平面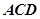 ,
,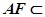 平面
平面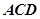 ,∴
,∴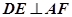
又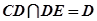 ,故
,故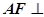 平面
平面
∵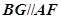 ,∴
,∴ 平面
平面
∵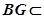 平面
平面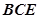 ,
,
∴平面 平面
平面 ………………………………………………………8分
………………………………………………………8分
(3)解:在平面 内,过
内,过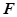 作
作 于
于 ,连
,连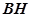
∵平面 平面
平面 ,∴
,∴ 平面
平面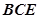
∴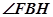 为
为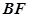 和平面
和平面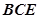 所成的角 ………………………………10分
所成的角 ………………………………10分
设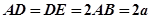 ,则
,则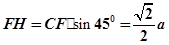
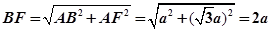 ,
,
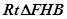 中,
中,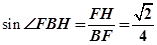
∴直线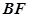 和平面
和平面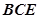 所成角的正弦值为
所成角的正弦值为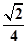 ………………………………………12分
………………………………………12分
(用空间向量法解答对应给分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面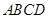 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在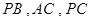 上,且
上,且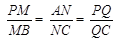
 ∥平面
∥平面 .
. 与平面面
与平面面
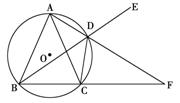

 平面BCD;
平面BCD;