题目内容
过点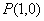 作曲线
作曲线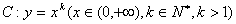 的切线,切点为
的切线,切点为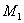 ,设
,设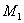 在
在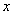 轴上的投影是点
轴上的投影是点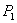 ;又过点
;又过点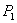 作曲线
作曲线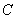 的切线,切点为
的切线,切点为 ,设
,设 在
在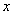 轴上的投影是点
轴上的投影是点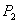 ;
; 依此下去,得到一系列点
依此下去,得到一系列点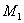 ,
, ,
,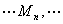 ;设它们的横坐标
;设它们的横坐标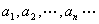 构成数列为
构成数列为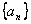 .
.
(1)求数列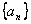 的通项公式;
的通项公式;
(2)求证: ;
;
(3)当 时,令
时,令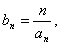 求数列
求数列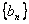 的前
的前 项和
项和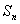 .
.
【答案】
解:(Ⅰ)对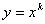 求导数,得
求导数,得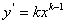 ,切点是
,切点是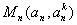 的切线方程是
的切线方程是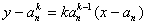 .…2分
.…2分
当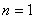 时,切线过点
时,切线过点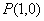 ,即
,即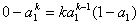 ,得
,得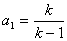 ;
;
当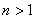 时,切线过点
时,切线过点 ,即
,即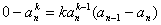 ,得
,得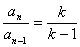 .
.
所以数列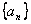 是首项
是首项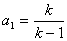 ,公比为
,公比为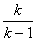 的等比数列,
的等比数列,
所以数列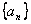 的通项公式为
的通项公式为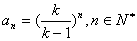 .………4分(文………6分)
.………4分(文………6分)
(1)应用二项式定理,得
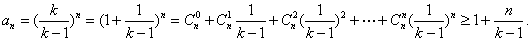 ………8分
………8分
(2)当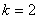 时,
时,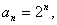 数列
数列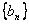 的前
的前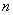 项和
项和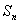 =
=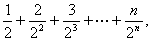
同乘以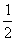 ,得
,得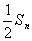 =
=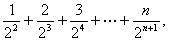 两式相减,………10分(文………8分)
两式相减,………10分(文………8分)
得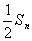 =
=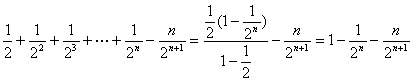 ,
,
所以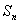 =
=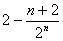 .………12分
.………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
