题目内容
设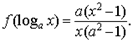
(1)求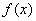 的表达式,并判断
的表达式,并判断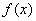 的奇偶性;
的奇偶性;
(2)试证明:函数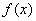 的图象上任意两点的连线的斜率大于0;
的图象上任意两点的连线的斜率大于0;
(3)对于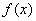 ,当
,当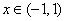 时,恒有
时,恒有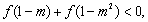 求m的取值范围。
求m的取值范围。
【答案】
(1) 奇函数
奇函数
(2)当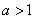 时,
时,
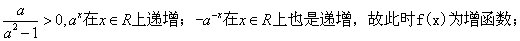
当 时,
时,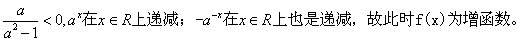 综上,
综上, 为增函数,由增函数的定义知:
为增函数,由增函数的定义知: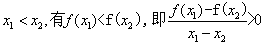 ,
,
故任意两点的连线斜率都大于零。(3)1<m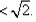
【解析】
试题分析:(1)令 代入
代入 中,得
中,得
 的定义域为R,关于原点对称。
的定义域为R,关于原点对称。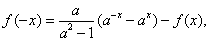

(2)当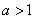 时,
时,
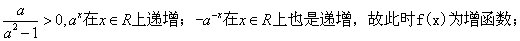
当 时,
时,
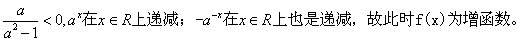 综上,
综上, 为增函数,由增函数的定义知:
为增函数,由增函数的定义知: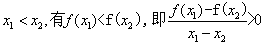 ,
,
故任意两点的连线斜率都大于零。
(3)由(1)知 为奇函数,由(2)知
为奇函数,由(2)知 在
在 为增函数,故有
为增函数,故有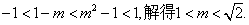
考点:本题考查了函数的性质的综合运用
点评:函数的单调性、奇偶性、周期性通常用于求解函数中的参数以及参数的范围,利用函数的性质往往能使问题简化

练习册系列答案
相关题目
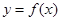 的图象经过原点,且
的图象经过原点,且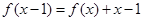 。
。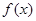 的表达式.
的表达式.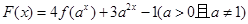 ,当
,当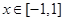 时,
时,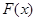 有最大值14,试求
有最大值14,试求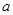 的值.
的值.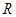 上的函数
上的函数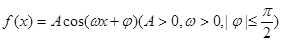 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为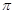 ,函数
,函数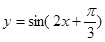 图象所有对称中心都在
图象所有对称中心都在 图象的对称轴上.
图象的对称轴上.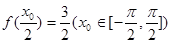 ,求
,求 的值;
的值;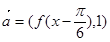 ,
,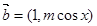 ,
, ,若
,若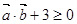 恒成立,求实数
恒成立,求实数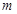 的取值范围.
的取值范围. 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ,
, 时,
时, ,求a,b的值.
,求a,b的值.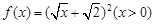 ,设正项数列
,设正项数列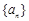 的首项
的首项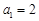 ,前n 项和
,前n 项和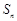 满足
满足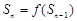 (
(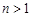 ,且
,且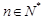 )。
)。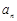 的表达式;
的表达式;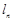 的斜率为
的斜率为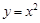 相切,
相切,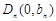 ,当
,当 ,若
,若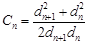 ,求数列
,求数列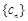 的前n 项和
的前n 项和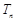 。
。