题目内容
若椭圆C1：
＋
＝1(0<b<2)的离心率等于
，抛物线C2：x2＝2py(p>0)的焦点在椭圆C1的顶点上．
(Ⅰ)求抛物线C2的方程；
(Ⅱ)若过M(－1,0)的直线l与抛物线C2交于E、F两点，又过E、F作抛物线C2的切线l1、l2，当l1⊥l2时，求直线l的方程．
【答案】
(Ⅰ)已知椭圆的长半轴长为a＝2，半焦距c，
由离心率e＝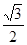
得，b2＝1.
∴椭圆的上顶点为(0,1)，即抛物线的焦点为(0,1)，
∴p＝2，抛物线的方程为x2＝4y.
(Ⅱ)由题知直线l的斜率存在且不为零，则可设直线l的方程为y＝k(x＋1)，E(x1，y1)，F(x2，y2)，
∵y＝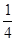
x2，∴y′＝
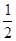x，
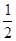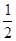∴切线l1，l2的斜率分别为x1，x2，
当l1⊥l2时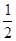，x1·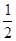x2＝－1，即x1·x2＝－4，
得：x2－4kx－4k＝0，
由Δ＝(－4k)2－4×(－4k)>0，解得k<－1或k>0.
又x1·x2＝－4k＝－4，得k＝1.
∴直线l的方程为x－y＋1＝0.
【解析】略
练习册系列答案
相关题目
，0)，B(
，－
)两点在椭圆C1：
＋
＝1(a＞b＞0)上，若椭圆C1的左焦点为F1，右焦点为F2，直线l1过点F1且垂直于椭圆的长轴，动直线l2垂直l1于点P，线段PF2垂直平分线交l2于点M，求点M的轨迹C2的方程．
＋
＝1(0＜b＜2)的离心率等于
，抛物线C2：x2＝2py(p＞0)的焦点在椭圆C1的顶点上．
＋
＝1(a1＞b1＞0)和椭圆C2：
＋
＝1(a2＞b2＞0)的焦点相同且a1＞a2．给出如下四个结论：
＞
；
；
＋y2＝1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是
