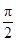题目内容
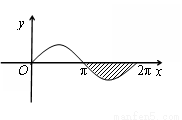
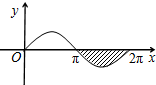
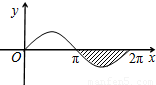
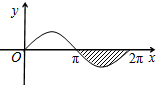 如图,阴影区域是由函数y=sinx的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )
如图,阴影区域是由函数y=sinx的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )分析:利用正弦函数图象的对称性可把所要求图形的面积转化为从x=0到x=π与x轴围成的面积,代入数据计算即可.
解答:解:根据正弦函数的对称性可得,
曲线从x=0到x=π与x轴围成的面积与从x=π到x=2π与x轴围成的面积相等,
∴由函数y=sinx的一段图象与x轴围成的封闭图形的面积
S=
sinxdx=-cosx
=2.
故选B.
曲线从x=0到x=π与x轴围成的面积与从x=π到x=2π与x轴围成的面积相等,
∴由函数y=sinx的一段图象与x轴围成的封闭图形的面积
S=
| ∫ | π 0 |
| | | π 0 |
故选B.
点评:本题主要考查了正弦函数的图象的对称性,从而转化为熟悉的图象解决,体现了转化思想的运用,解答本题的关键是灵活运用性质,对问题灵活转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
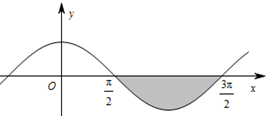
如图,阴影区域是由函数y=cosx的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )

| A、1 | ||
| B、2 | ||
C、
| ||
| D、π |
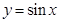 的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )
的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )