题目内容
已知一个圆同时满足下列条件:①与x轴相切;②圆心在直线3x-y=0上;③被直线l:x-y=0截得的弦长为2
,则此圆的方程为
| 7 |
(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9
(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9
.分析:根据题意,设圆心为C(a,3a),圆C被直线l截得的弦为AB,D为AB的中点,连结CD、BC.由垂径定理和点到直线的距离公式,建立关于a的方程并解出a值,即可得到满足条件的圆的标准方程.
解答:解: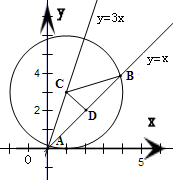 当圆心在直线3x-y=0上的第一象限部分时,设圆心为C(a,3a),其中a>0,
当圆心在直线3x-y=0上的第一象限部分时,设圆心为C(a,3a),其中a>0,
∵圆C与x轴相切,∴C到x轴的距离等于半径r,可得r=3a.
设直线l交圆C于A、B两点,D为AB的中点,连结BC、CD,则CD⊥AB,
又∵圆C被直线l:x-y=0截得的弦长为2
,
∴Rt△BCD中,|BC|=r=3a,|BD|=
可得|CD|=
=
.
根据点到直线的距离公式,得|CD|=
=
a,
∴
=
a,解之得a=1,
可得点C(1,3),半径r=3,此时圆C的方程为(x-1)2+(y-3)2=9;
同理可得:当圆心在直线3x-y=0上的第三象限部分时,圆C的方程为(x+1)2+(y+3)2=9.
综上所述,所求圆的标准方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.
 当圆心在直线3x-y=0上的第一象限部分时,设圆心为C(a,3a),其中a>0,
当圆心在直线3x-y=0上的第一象限部分时,设圆心为C(a,3a),其中a>0,∵圆C与x轴相切,∴C到x轴的距离等于半径r,可得r=3a.
设直线l交圆C于A、B两点,D为AB的中点,连结BC、CD,则CD⊥AB,
又∵圆C被直线l:x-y=0截得的弦长为2
| 7 |
∴Rt△BCD中,|BC|=r=3a,|BD|=
| 7 |
可得|CD|=
| |BC|2-|BD|2 |
| 9a2-7 |
根据点到直线的距离公式,得|CD|=
| |a-3a| | ||
|
| 2 |
∴
| 9a2-7 |
| 2 |
可得点C(1,3),半径r=3,此时圆C的方程为(x-1)2+(y-3)2=9;
同理可得:当圆心在直线3x-y=0上的第三象限部分时,圆C的方程为(x+1)2+(y+3)2=9.
综上所述,所求圆的标准方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.
点评:本题给出圆满足的条件,求圆的标准方程.着重考查了圆的标准方程、点到直线的距离公式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,同时满足下列三个条件:
,同时满足下列三个条件: 有相同的最小正周期;
有相同的最小正周期; 后关于y轴对称;
后关于y轴对称; 有相同的最小值。
有相同的最小值。 的解析式是 。
的解析式是 。 是同时满足下列两个性质的函数
是同时满足下列两个性质的函数 组成的集合:
组成的集合: ,使得
,使得 .
. 是否属于集合
是否属于集合
 ,求实数
,求实数 的取值范围.
的取值范围.