题目内容
设a∈R,f(x)为奇函数,且f(2x)=
.
(1)求a的值及f(x)的解析式和值域;
(2)g(x)=log
,若x∈[
,
]时,log2
≤g(x)恒成立,求实数k的取值范围.
| a•4x-a-2 |
| 4x+1 |
(1)求a的值及f(x)的解析式和值域;
(2)g(x)=log
| 2 |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
| 1+x |
| 1-x |
分析:(1)由奇函数的特性f(0)=0,解出a=1可得f(x)的解析式为f(x)=
.再由指数函数的值域,解关于y的不等式即可求出f(x)的值域;
(2)将原不等式化简,可得log2
≤2log2
对x∈[
,
]恒成立,由此结合对数函数的单调性和定义域,化简得到k2≤1-x2对于x∈[
,
]恒成立,可得实数k的取值范围.
| 2x-1 |
| 2x+1 |
(2)将原不等式化简,可得log2
| 1+x |
| 1-x |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解答:解:(1)令t=2x,得f (x)=
-------------------------------(1分)
∵f (x)是奇函数,∴f(0)=0,解之可得a=1
∴函数的解析式为f(x)=
-----------------------------(3分)
∵由y=
解出2x=
>0,解之得-1<y<1
∴值域为 (-1,1)-------------------------------------------------(6分)
(2)log2
≤log
对x∈[
,
]恒成立
即:log2
≤
,
不等式log2
≤2log2
对x∈[
,
]恒成立------(8分)
即
----①,对于x∈[
,
]恒成立
由①,得k2≤1-x2对于x∈[
,
]恒成立---------------------------(10分)
∴k2≤1-
=
,解之得0<k≤
----------------------------------(12分)
| a•2x-a-2 |
| 2x+1 |
∵f (x)是奇函数,∴f(0)=0,解之可得a=1
∴函数的解析式为f(x)=
| 2x-1 |
| 2x+1 |
∵由y=
| 2x-1 |
| 2x+1 |
| 1+y |
| 1-y |
∴值域为 (-1,1)-------------------------------------------------(6分)
(2)log2
| 1+x |
| 1-x |
| 2 |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
即:log2
| 1+x |
| 1-x |
log2
| ||
log2
|
不等式log2
| 1+x |
| 1-x |
| 1+x |
| k |
| 1 |
| 2 |
| 2 |
| 3 |
即
|
| 1 |
| 2 |
| 2 |
| 3 |
由①,得k2≤1-x2对于x∈[
| 1 |
| 2 |
| 2 |
| 3 |
∴k2≤1-
| 4 |
| 9 |
| 5 |
| 9 |
| ||
| 3 |
点评:本题给出含有指数式的分式型函数,求函数的奇偶性和值域,并依此讨论不等式恒成立时实数k的范围.着重考查了基本初等函数的单调性、奇偶性和函数恒成立问题等知识,属于中档题.

练习册系列答案
相关题目
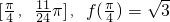 .给出下列几个命题:
.给出下列几个命题: 处取得小值;
处取得小值;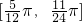 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间; .
.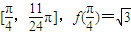 .给出下列几个命题:
.给出下列几个命题: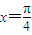 处取得小值;
处取得小值;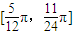 是f(x)的一个单调递减区间;
是f(x)的一个单调递减区间;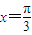 .
.