题目内容
若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
C
设a与b的夹角为θ,
则(2a+b)·b=2a·b+b2="2|a||b|cos" θ+|b|2
=|b|2(2cos θ+1)=0,
又b为非零向量,∴2cos θ+1=0,
∴cos θ=-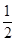 ,∴θ=120°.故选C.
,∴θ=120°.故选C.
则(2a+b)·b=2a·b+b2="2|a||b|cos" θ+|b|2
=|b|2(2cos θ+1)=0,
又b为非零向量,∴2cos θ+1=0,
∴cos θ=-
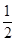 ,∴θ=120°.故选C.
,∴θ=120°.故选C.
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
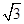 ,点P为边BC所在直线上的一个动点,则关于
,点P为边BC所在直线上的一个动点,则关于 ·(
·(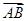 +
+ )的值,下列选项正确的是( )
)的值,下列选项正确的是( ) ,若向量b1=e1-2e2,b2=3e1+4e2,则b1·b2=________.
,若向量b1=e1-2e2,b2=3e1+4e2,则b1·b2=________.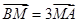 ,则
,则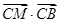 =( )
=( )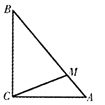
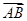 ·
·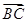 =1,则BC=( ).
=1,则BC=( ).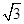
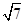
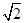
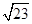
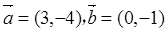 ,则向量
,则向量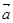 在向量
在向量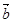 的方向上的投影是 .
的方向上的投影是 .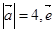 为单位向量,当
为单位向量,当 的夹角为
的夹角为 时,
时,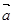 在
在 上的投影为( )
上的投影为( )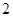
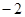


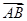 ·
·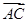 = .
= .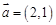 ,
,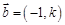 ,若
,若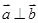 ,则实数
,则实数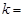 ______;
______;