题目内容
在△ABC中，若（a+b+c）（b+c-a）=3bc，则A=
- A.90°
- B.60°
- C.135°
- D.150°
B
分析：把已知条件的左边利用平方差公式化简后，与右边合并即可得到b2+c2-a2=bc，然后利用余弦定理表示出cosA的式子，把化简得到的b2+c2-a2=bc代入即可求出cosA的值，然后根据A的范围，利用特殊角的三角函数值即可求出A的度数．
解答：由（a+b+c）（b+c-a）=（b+c）2-a2=b2+2bc+c2-a2=3bc，
化简得：b2+c2-a2=bc，
则根据余弦定理得：cosA=
=
=
，
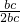又A∈（0，180°），所以A=60°．
故选B
点评：此题考查学生灵活运用余弦定理化简求值，考查了整体代换的数学思想，是一道综合题．
分析：把已知条件的左边利用平方差公式化简后，与右边合并即可得到b2+c2-a2=bc，然后利用余弦定理表示出cosA的式子，把化简得到的b2+c2-a2=bc代入即可求出cosA的值，然后根据A的范围，利用特殊角的三角函数值即可求出A的度数．
解答：由（a+b+c）（b+c-a）=（b+c）2-a2=b2+2bc+c2-a2=3bc，
化简得：b2+c2-a2=bc，
则根据余弦定理得：cosA=
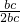==，又A∈（0，180°），所以A=60°．
故选B
点评：此题考查学生灵活运用余弦定理化简求值，考查了整体代换的数学思想，是一道综合题．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
在△ABC中，若
=
，
=
，
=
且
•
=
•
=
•
，则△ABC的形状是△ABC的（ ）
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
如图，在△ABC中，若在△ABC中，若（a+b+c）（b+c-a）=3bc，且sinA=2sinBcosC，则△ABC的形状是（ ）
| A、直角三角形 | B、等腰直角三角形 | C、等腰三角形 | D、等边三角形 |