题目内容
是否存在这样的平移,使抛物线y=-x2平移后过原点,且以平移后的抛物线的顶点和它与x轴的两个交点为顶点的三角形的面积为1?若不存在,请说明理由;若存在,求出平移后抛物线的解析式.
解:假设存在这样的平移向量a=(h,k).
将平移公式代入y=-x2得平移后的抛物线为
y-k=-(x-h)2,即y=-(x-h)2+k.
∵平移后抛物线过原点,
∴k=h2.①
由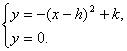
得(x-h)2=k.
∴当k>0时,x=h±![]() .
.
因此抛物线在x轴上截得的弦长为2![]() .
.
又∵平移后抛物线的顶点为(h,k),
∴依题意![]() ·2
·2![]() ·k=1(k>0).
·k=1(k>0).
则k=1.②
将②代入①,得h=±1.
∴存在满足已知条件的平移向量a=(1,1)或a=(-1,1).
当a=(1,1)时,平移后抛物线的解析式为
y=-(x-1)2+1,即y=-x2+2x;
当a=(-1,1)时,平移后抛物线的解析式为
y=-(x+1)2+1,即y=-x2-2x.
点评:本题考查函数图象的平移,待定系数法求函数解析式,函数的性质等知识.逐步掌握对探索性问题的一般解法.

练习册系列答案
相关题目
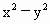 =k的中心在直线l:y=x上移动,且保持对称轴平行于坐标轴,问平移中是否存在这样的双曲线,它截直线l的弦长,与截y轴的弦长都等于2
=k的中心在直线l:y=x上移动,且保持对称轴平行于坐标轴,问平移中是否存在这样的双曲线,它截直线l的弦长,与截y轴的弦长都等于2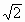 ?若存在,求出双曲线方程;若不存在,说明理由.
?若存在,求出双曲线方程;若不存在,说明理由.