题目内容
为了研究子女吸烟与父母吸烟的关系,调查了1520青少年及其家长,得数据如下
附表:
|
分析:本题考查的知识点是独立性检验的应用,我们可以根据列联表中的数据,代入公式K2=
,计算出k值,然后代入离散系数表,比较即可得到答案.
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
解答:解:∵K2=
=
≈32.52>10.828.
故我们有99.9%的把握说子女吸烟与父母吸烟有关
故选D.
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 1520×(237×522-83×678)2 |
| 915×605×320×1200 |
故我们有99.9%的把握说子女吸烟与父母吸烟有关
故选D.
点评:独立性检验的应用的步骤为:根据已知条件将数据归结到一个表格内,列出列联表,再根据列联表中的数据,代入公式K2=
,计算出k值,然后代入离散系数表,比较即可得到答案.
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |

练习册系列答案
相关题目
为了研究子女吸烟与父母吸烟的关系,调查了1520青少年及其家长,得数据如下

则下列结论较准确的一个是( )

则下列结论较准确的一个是( )
| A、子女吸烟与父母吸烟无关 | B、有95%的把握说子女吸烟与父母吸烟有关 | C、有99%的把握说子女吸烟与父母吸烟有关 | D、有99.9%的把握说子女吸烟与父母吸烟有关 |
为了研究子女吸烟与父母吸烟的关系,调查了 青少年及其家长,得数据如下
青少年及其家长,得数据如下
|
|
父母吸烟 |
父母不吸烟 |
合计 |
|
子女吸烟 |
237 |
83 |
320 |
|
子女不吸烟 |
678 |
522 |
1200 |
|
合计 |
915 |
605 |
1520 |
则下列结论较准确的一个是 ( )
A.子女吸烟与父母吸烟无关
B.有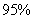 的把握说子女吸烟与父母吸烟有关
的把握说子女吸烟与父母吸烟有关
C.有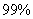 的把握说子女吸烟与父母吸烟有关
的把握说子女吸烟与父母吸烟有关
D.有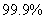 的把握说子女吸烟与父母吸烟有关
的把握说子女吸烟与父母吸烟有关
为了研究子女吸烟与父母吸烟的关系,调查了一千多名青少年及其家长,数据如下:?
| 父母吸烟 | 父母不吸烟 | 总 计 |
子女吸烟 | 237 | 83 | 320 |
子女不吸烟 | 678 | 522 | 1 200 |
总 计 | 915 | 605 | 1 520 |
分别利用图形和独立性检验方法判断父母吸烟对子女是否吸烟有影响.
