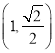题目内容
【题目】随机抽取某校高一100名学生的期末考试英语成绩(他们的英语成绩都在80分![]() 140分之间),将他们的英语成绩(单位:分)分成:
140分之间),将他们的英语成绩(单位:分)分成:![]() ,
,![]() ,
,![]() ,
,![]() ,
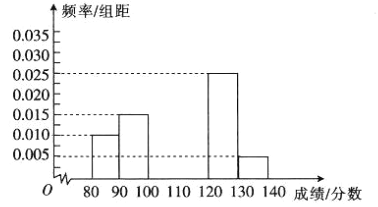
,![]() 六组,得到如图所示的部分频率分布直方图,已知成绩处于
六组,得到如图所示的部分频率分布直方图,已知成绩处于![]() 内与
内与![]() 内的频数之和等于成绩处于
内的频数之和等于成绩处于![]() 内的频数,根据图中的信息,回答下列问题:
内的频数,根据图中的信息,回答下列问题:
(1)求频率分布直方图中未画出的小矩形的面积之和;
(2)求成绩处于![]() 内与
内与![]() 内的频率之差;
内的频率之差;
(3)用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本,将该样本看成一个总体,从中任选2人,记这2人中成绩低于130分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)0.45;(2)0.15;(3)见解析.
【解析】
(1)根据频率分布直方图中,所有小矩形面积和为1,所以剩余小矩形的面积等于1减去已知小矩形的面积。
(2)根据频率之和等于概率,可得关于a、b的方程组,解方程组即可求得a、b的值,进而得到频率差。
(3)根据事件X分布,可知X的所有可能为1,2。分别求得两种情况下的概率,即可得分布列,进而求得期望。
(1)由题意可知,成绩处于![]() 内的概率为
内的概率为![]()
所以频率分布直方图中未画出的小矩形的面积之和为0.45
(2)设成绩处于![]() 与
与![]() 内的频率分别为
内的频率分别为![]() ,
,
因为成绩处于![]() 内与
内与![]() 内的概率之和等于成绩处于
内的概率之和等于成绩处于![]() 内的频率,
内的频率,
所以成绩处于![]() 内与
内与![]() 内的概率之和等于成绩处于
内的概率之和等于成绩处于![]() 内的概率,
内的概率,
所以![]() ,解得
,解得![]()
所以成绩处于![]() 内与
内与![]() 内的频率之差为
内的频率之差为![]()
(3)由题可知,成绩处于![]() 内的学生数为
内的学生数为![]() ,成绩处于
,成绩处于![]() 内的学生数为
内的学生数为![]() ,所以用分层抽样的方法从身高不低于120分的学生中选取一个容量为6的样本,需从成绩处于
,所以用分层抽样的方法从身高不低于120分的学生中选取一个容量为6的样本,需从成绩处于![]() 内的学生中选取5人,从成绩处于
内的学生中选取5人,从成绩处于![]() 内的学生中选取1人,易知
内的学生中选取1人,易知![]() 的所有可能取值是1,2,
的所有可能取值是1,2,
![]()
![]()
所以随机变量![]() 的分布列为
的分布列为
X | 1 | 2 |
P |
|
|
所以![]() .
.

【题目】从一批草莓中,随机抽取![]() 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
分组(重量) |
|
|
|
|
频数(个) |
|
|
|
|
已知从![]() 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在![]() 的草莓的概率为
的草莓的概率为![]() .
.
(1)求出![]() ,
,![]() 的值;
的值;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的草莓中共抽取
的草莓中共抽取![]() 个,再从这
个,再从这![]() 个草莓中任取
个草莓中任取![]() 个,求重量在
个,求重量在![]() 和
和![]() 中各有
中各有![]() 个的概率.
个的概率.