题目内容
已知离散型随机变量X的分布列为P(X=
)=ak(k=1,2,3,4,5),则P(X≥
)为( )
| k |
| 5 |
| 3 |
| 5 |
分析:由题意根据离散型随机变量的概率分布列的性质可得a+2a+3a+4a+5a=1,由此解得a的值.再根据P(X≥
)=3a+4a+5a,运算求得结果.
| 3 |
| 5 |
解答:解:由题意根据离散型随机变量的概率分布列的性质可得 a+2a+3a+4a+5a=1,解得 a=
.
∴P(X≥
)=P(X=3)+P(X=
)+P(X=1)=3a+4a+5a=12a=
,
故选D.
| 1 |
| 15 |
∴P(X≥
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
故选D.
点评:本题主要考查离散型随机变量的概率分布列的性质的应用,属于中档题.

练习册系列答案
相关题目
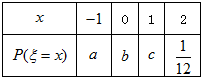 已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=
已知离散型随机变量x的分布列如右表.若Eξ=0,Dξ=1,则符合条件的一组数(a,b,c)=