题目内容
已知抛物线的顶点为椭圆
+
=1(a>b>0)的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行.又抛物线与椭圆交于点M(
,-
),求抛物线与椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
2
| ||
| 3 |
分析:设出抛物线方程,代入M的坐标,可得抛物线的方程,利用椭圆的离心率是抛物线离心率的一半,代入M的坐标,求得几何量,即可得到结论.
解答:解:由题意,设抛物线的方程为y2=2px(p>0),则
将M(
,-
)代入方程可得
=2p×
,∴p=2,
∴抛物线的方程为y2=4x
∵椭圆的离心率是抛物线离心率的一半,
∴e=
=
∵
+
=1,a2=b2+c2
∴a=2,b=
∴椭圆方程为:
+
=1
将M(
| 2 |
| 3 |
2
| ||
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
∴抛物线的方程为y2=4x
∵椭圆的离心率是抛物线离心率的一半,
∴e=
| c |
| a |
| 1 |
| 2 |
∵
| ||
| a2 |
| ||
| b2 |
∴a=2,b=
| 3 |
∴椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题考查抛物线、椭圆的标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
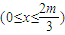 和椭圆弧
和椭圆弧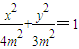

 和椭圆弧
和椭圆弧
