题目内容
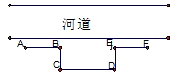 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最小值,并求出这个最小值.
解:(1)由题意,y=2BC+CD+20=2x+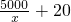 (x>0),即y=2x+
(x>0),即y=2x+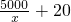 (x>0);
(x>0);
(2)令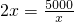 ,可得x=50∉(0,40],
,可得x=50∉(0,40],
因为y=2x+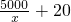 在(0,40)内递减,
在(0,40)内递减,
所以y的最小值为f(40)=225m,此时x=40m.
分析:(1)根据y=2BC+CD+20,可建立y关于x的函数解析式y=f(x);
(2)确定函数在(0,40)内递减,即可求得函数的最小值,及相应的x的值.
点评:本题考查函数模型的构建,考查函数的单调性,考查函数的最值,正确确定函数的解析式是关键.
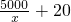 (x>0),即y=2x+
(x>0),即y=2x+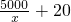 (x>0);
(x>0);(2)令
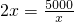 ,可得x=50∉(0,40],
,可得x=50∉(0,40],因为y=2x+
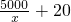 在(0,40)内递减,
在(0,40)内递减,所以y的最小值为f(40)=225m,此时x=40m.
分析:(1)根据y=2BC+CD+20,可建立y关于x的函数解析式y=f(x);
(2)确定函数在(0,40)内递减,即可求得函数的最小值,及相应的x的值.
点评:本题考查函数模型的构建,考查函数的单调性,考查函数的最值,正确确定函数的解析式是关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
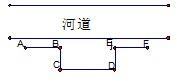 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求
为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为xm时,所砌砖墙的总长度为ym,且在计算时,不计砖墙的厚度,求