题目内容
数列![]() 满足
满足![]()
![]()
(I)求![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,
,![]() ,
,![]() ,
,
求使![]() 的所有k的值,并说明理由。
的所有k的值,并说明理由。
(I)数列![]() 的通项公式为
的通项公式为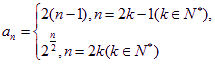 (2)满足
(2)满足![]() 的所有k的值为3,4,5.
的所有k的值为3,4,5.
解析:
(I)因为![]() 所以
所以![]()
![]() 一般地,
一般地,
当![]() 时,
时,
![]()
即![]() 所以数列
所以数列![]() 是首项为0、公差为4的等差数列,
是首项为0、公差为4的等差数列,
因此![]()
当![]() 时,
时,![]()
所以数列![]() 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此![]()
故数列![]() 的通项公式为
的通项公式为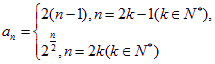
(II)由(I)知,![]()
![]()
![]()
于是![]()
![]()
![]()
![]()
![]()
![]() .
.
下面证明: 当![]() 时,
时,![]() 事实上, 当
事实上, 当![]() 时,
时,
![]() 即
即![]()
又![]() 所以当
所以当![]() 时,
时,![]()
故满足![]() 的所有k的值为3,4,5.
的所有k的值为3,4,5.

练习册系列答案
相关题目
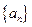 满足
满足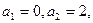
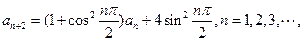
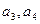 ,并求数列
,并求数列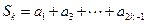 ,
,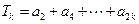 ,
,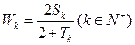 ,
,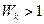 的所有k的值,并说明理由。
的所有k的值,并说明理由。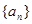 的前n项和
的前n项和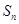 满足
满足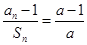 (
(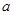 >0,且
>0,且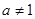 )。数列
)。数列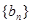 满足
满足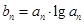
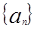 的通项。
的通项。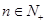 都有
都有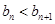 ,求
,求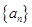 满足
满足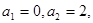
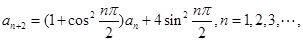
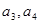 ,并求数列
,并求数列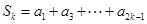 ,
,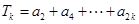 ,
,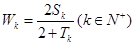 ,
,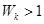 的所有k的值,并说明理由。
的所有k的值,并说明理由。