题目内容

如图，AB是圆O的直径，CA垂直圆O所在的平面，D是圆周上一点，已知AC=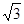。AD=。

（Ⅰ）求证：平面ADC⊥平面CDB;（Ⅱ）求平面CDB与ADB所成的二面角的正切值。

【答案】

（Ⅰ）∵CA⊥平面ADB ∴CA⊥BD，又D是圆周上一点，故BD⊥AD∴BD⊥平面ACD ∵BD平面BCD ∴平面CDB⊥平面CAD

（Ⅱ）又（Ⅰ）知BD⊥平面ADC， ∴BD⊥AD，BD⊥CD，故∠CDA就是二面角C—DB—A的平面角。又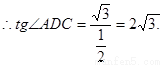，，∴平面ADB与平面ADC所成二面角的平面角的正切值为。

【解析】略

练习册系列答案

单元期中期末试卷系列答案

导学教程高中新课标系列答案

过关检测同步活页试卷系列答案

交大之星课后练系列答案

名师导航好卷100分系列答案

培优名卷系列答案

上海达标卷好题好卷系列答案

小学课时特训系列答案

1加1轻巧夺冠小专家课时练练通系列答案

校缘自助课堂系列答案

相关题目

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
（1）求证：平面ACD⊥平面ADE；
（2）若AB=2，BC=1，tan∠EAB=

，求几何体EDABC的体积V．

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

A．（参数方程与极坐标）

直线与直线的夹角大小为

B．（不等式选讲）要使关于x的不等式在实数

范围内有解，则A的取值范围是

C．（几何证明选讲）如图所示，在圆O中，AB是圆O的直

径AB =8,E为OB．的中点，CD过点E且垂直于AB,

EF⊥AC,则

CF•CA=