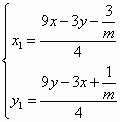题目内容
设点P(x0,y0)在直线x=m(y≠±m,0<m<1)上,过点P作双曲线x2-y2=1的两条切线PA、PB,切点为A、B,定点![]() .
.
(1)求证:三点A、M、B共线.
(2)过点A作直线x-y=0的垂线,垂足为N,试求△AMN的重心G所在曲线方程.
答案:
解析:
解析:
|
证明:(1)设 设切线 从而 因此 同理 又 即点 又
(2)垂线 由 所以 由 |

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
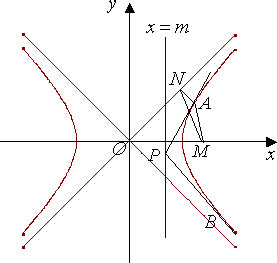
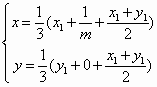 解得
解得