题目内容
某企业生产A、B两种产品，A产品的利润为60元/件，5产品的利润为80元/件，两种产品都需要在加工车间和装配车间进行生产．每件A产品在加工车间和装配车间各需经过0.8h和2.4h，每件5产品在加工车间和装配车间都需经过1.6h．在一个生产周期中，加工车间最大加工时间为240h，装配车间最大生产时间为288h，在销路顺畅无障碍的情况下，该企业在一个生产周期内可获得的最大利润是（ ）
| A、12400元 | B、12600元 | C、12800元 | D、13000元 |
分析：先设设该企业生产A产品为x 件，B产品为y件，列出约束条件，再根据约束条件画出可行域，设z=60x+80y，再利用z的几何意义求最值，只需求出直线z=60x+80y过可行域内的点时，从而得到z值即可．
解答：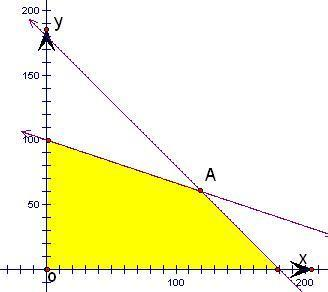
解：设该企业生产A产品为x 件，B产品为y件，则该企业可获得利润为z=60x+80y，
且
由图可知，最优解为A（120，60），
∴z的最大值为z=60×120+80×60=13000（元）．
故选D．
解：设该企业生产A产品为x 件，B产品为y件，则该企业可获得利润为z=60x+80y，且
|
由图可知，最优解为A（120，60），
∴z的最大值为z=60×120+80×60=13000（元）．
故选D．
点评：在解决线性规划的应用题时，其步骤为：①分析题目中相关量的关系，列出不等式组，即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
