题目内容
已知直线l1的方程为y=x，直线l2的方程为ax-y=0（a为实数）．当直线l1与直线l2的夹角在（0，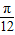
）之间变动时，a的取值范围是（ ）A．（
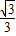，1）∪（1，
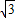）B．（
，
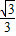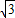）C．（0，1）
D．（1，
）
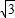【答案】分析：设出两条直线的夹角，利用夹角公式求出关于a的表达式，即可求出a的范围．
解答：解：：设直线l1与直线l2的夹角为θ，所以tanθ=|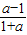
|，
因为直线l1与l2夹角的范围为（0，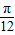
），所以tanθ∈（0，2-
），
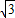所以0＜|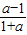
|＜2-
，
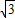解得：a∈（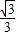
，1）∪（1，
）．
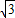故选A．
点评：本题考查两条直线的夹角的求法，考查绝对值不等式的解法，考查计算能力，属于中档题．
解答：解：：设直线l1与直线l2的夹角为θ，所以tanθ=|
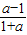|，因为直线l1与l2夹角的范围为（0，
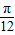），所以tanθ∈（0，2-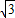），所以0＜|
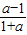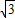|＜2-，解得：a∈（
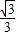，1）∪（1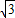，）．故选A．
点评：本题考查两条直线的夹角的求法，考查绝对值不等式的解法，考查计算能力，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
已知直线l1的方程为y=x，直线l2的方程为y=ax+b（a，b为实数），当直线l1与l2夹角的范围为[0，
）时，a的取值范围是（ ）
| π |
| 12 |
A、（
| ||||||
| B、（0，1） | ||||||
C、（
| ||||||
D、（1，
|