Question

（本小题满分12分，（Ⅰ）问5分，（Ⅱ）问7分）

已知以原点为中心的椭圆的一条准线方程为，离心率，是椭圆上的动点。

（Ⅰ）若的坐标分别是，求的最大值；

（Ⅱ）如题（20）图，点的坐标为，是圆上的点，是点在轴上的射影，点满足条件：，，求线段的中点的轨迹方程。

Answer 1

（Ⅰ）4

（Ⅱ）

解析:

（Ⅰ）由题设条件知焦点在y轴上，故设椭圆方程为（a ＞b＞ 0 ）。

设，由准线方程得，由得，解得 a = 2 ，c = ，从而 b = 1，椭圆方程为。

又易知C，D两点是椭圆的焦点，所以,。

从而，当且仅当，即点M的坐标为　时上式取等号，的最大值为4。

（II）如答（20）图，设，。

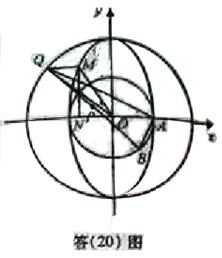
因为，故

       ①

 因为

 

所以   .     ②

记P点的坐标为，因为P是BQ的中点

所以    

由因为  ，结合①，②得

      

      

      

故动点P的估计方程为

。