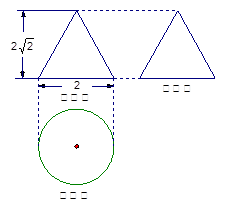
题目内容
棱长为 的正四面体内切一球,然后在正四面体和该球形成的空隙处各放入一小球,则这些球的最大半径为( )
的正四面体内切一球,然后在正四面体和该球形成的空隙处各放入一小球,则这些球的最大半径为( )
A. | B. | C. | D. |
C
解析

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知正方体的外接球的体积是 ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )
A. | B. | C. | D. |
某三棱锥的三视图如图所示,该三棱锥的表面积是( )
A. | B. |
C. | D. |
一个几何体的三视图如图所示,则该几何体的体积为( )
| A.12 | B.11 | C. | D. |
一个空间几何体的三视图如图所示,则该几何体的表面积为 ( )
| A.48 | B. |
C. | D.80 |
已知三棱锥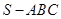 中,底面
中,底面 为边长等于2的等边三角形,
为边长等于2的等边三角形, 垂直于底面
垂直于底面 ,
, =1,那么直线
=1,那么直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为


A. | B. | C. | D. |
 中,
中, 分别为棱
分别为棱 的中点,在平面
的中点,在平面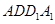 内且与平面
内且与平面 平行的直线( )
平行的直线( )