题目内容
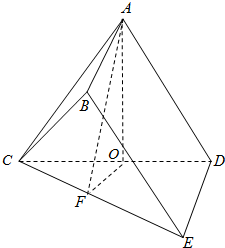 已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,AB=1,AC=AD=CD=DE=2,F、O分别为CE、CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,AB=1,AC=AD=CD=DE=2,F、O分别为CE、CD的中点.(Ⅰ)求证:CD⊥面AFO;
(Ⅱ)求三棱锥C-ADE的体积.
分析:(I)根据已知中AB⊥平面ACD,DE∥AB,F、O分别为CE、CD的中点,AC=AD=CD=DE=2,我们易得到CD与面AFO中两条相交直线AO、FO均垂直,根据线面垂直的判定定理,即可得到答案.
(II)根据(1)的结论,我们易判断AO即为平面CDE上的高,由此计算出三角形CDE的面积,代入棱锥体积公式即可求解.
(II)根据(1)的结论,我们易判断AO即为平面CDE上的高,由此计算出三角形CDE的面积,代入棱锥体积公式即可求解.
解答: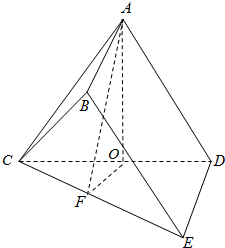 解:(I)∵AB⊥平面ACDDE∥AB
解:(I)∵AB⊥平面ACDDE∥AB
∴DE⊥平面ACD
∴DE⊥CD
∵F、O分别为CE、CD的中点.
∴FO∥ED
∴FO⊥CD
∵△ACD是等边三角形
∴AO⊥CD
∴CD⊥面AFO(6分)
(II)∵AO⊥CD,△ACD是等边三角形
∴AO⊥面CDE
∴AO是三棱锥A-CDE的高
∴VC-ADE=VA-CDE=
S△CDE•AO=
×
×2×2×
=
(12分)
 解:(I)∵AB⊥平面ACDDE∥AB
解:(I)∵AB⊥平面ACDDE∥AB∴DE⊥平面ACD
∴DE⊥CD
∵F、O分别为CE、CD的中点.
∴FO∥ED
∴FO⊥CD
∵△ACD是等边三角形
∴AO⊥CD
∴CD⊥面AFO(6分)
(II)∵AO⊥CD,△ACD是等边三角形
∴AO⊥面CDE
∴AO是三棱锥A-CDE的高
∴VC-ADE=VA-CDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:本题考查的知识点是棱锥的体积,直线与平面垂直的判定,掌握线面垂直的判定定理,找出棱锥的高和底面积,是解答本题的关键.

练习册系列答案
相关题目
 如图,已知多面体ABCDE中,AE⊥平面ABC,AE
如图,已知多面体ABCDE中,AE⊥平面ABC,AE 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.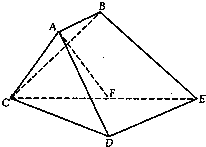 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点. 如图,已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.