题目内容
两个相同的正四棱锥组成如右图所示的几何体,可放在棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有

[ ]
A.1个
B.2个
C.3个
D.无穷多个
答案:D
解析:

解析:
解法一:八面体上、下两顶点间距离即两正四棱锥高之和为定值1,则本题可以转化为一个正方形可以有多少个内接正方形,显然有无穷多个.其面积变化,体积显然变化.应选D.
解法二:如下图所示,在正方体的俯视图中,可得正八面体中截面正方形ABCD内接于另一个正方形,由此知正方形ABCD的面积的范围为S∈[![]() ,1),∴八面体的体积V=
,1),∴八面体的体积V=![]() S×1∈[
S×1∈[![]() ,
,![]() ),即其体积的可能值有无穷多个.故应选D.
),即其体积的可能值有无穷多个.故应选D.


练习册系列答案
相关题目
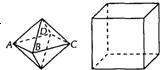



 两个相同的正四棱锥组成如图所示的几何体,可放入棱
两个相同的正四棱锥组成如图所示的几何体,可放入棱 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为