题目内容
已知函数f（x）=x2+4x+3，（1）若g（x）=f（x）-cx为偶函数，求c．
（2）用定义证明：函数f（x）在区间[-2，+∞）上是增函数；并写出该函数的值域．
【答案】分析：（1）由题意可得g（-x）=g（x），代入可求c
（2）由（1）可得f（x），利用单调性的定义，要证明数f（x）在区间[-2，+∞）上是增函数，只要当-2≤x1＜x2 时有f（x2）＞f（x1）即可
故由已证f（x）在[-2，+∞）单调递增 可得f（x）min=f（-2）=-1可求
解答：解：（1）∵g（x）=f（x）-cx=x2+（4-c）x+3为偶函数
∴g（-x）=g（x）
∴（-x）2+（4-c）（-x）+3=x2+（4-c）x+3 …（2分）
∴4-c=-（4-c）
∴c=4 …（5分）
（2）证明：设-2≤x1＜x2 …（6分）
则f（x2）-f（x1）=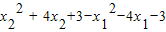
=（x1+x2）（x2-x1）+4（x2-x1）
=（x2-x1）（x1+x2+4）…（8分）
∵-2≤x1＜x2
∴x2-x1＞0且x1+x2+4＞0
∴f（x2）-f（x1）＞0即f（x2）＞f（x1）
故 f（x）在[-2，+∞）单调递增 …（10分）
f（x）min=f（-2）=-1
所以函数的值域为[-1，+∞） …（12分）
点评：本题主要考查了偶函数的定义的应用，函数的单调性的定义在证明（判断）函数的单调性中的应用，属于基本知识的简单的应用
（2）由（1）可得f（x），利用单调性的定义，要证明数f（x）在区间[-2，+∞）上是增函数，只要当-2≤x1＜x2 时有f（x2）＞f（x1）即可
故由已证f（x）在[-2，+∞）单调递增 可得f（x）min=f（-2）=-1可求
解答：解：（1）∵g（x）=f（x）-cx=x2+（4-c）x+3为偶函数
∴g（-x）=g（x）
∴（-x）2+（4-c）（-x）+3=x2+（4-c）x+3 …（2分）
∴4-c=-（4-c）
∴c=4 …（5分）
（2）证明：设-2≤x1＜x2 …（6分）
则f（x2）-f（x1）=
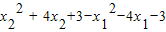
=（x1+x2）（x2-x1）+4（x2-x1）
=（x2-x1）（x1+x2+4）…（8分）
∵-2≤x1＜x2
∴x2-x1＞0且x1+x2+4＞0
∴f（x2）-f（x1）＞0即f（x2）＞f（x1）
故 f（x）在[-2，+∞）单调递增 …（10分）
f（x）min=f（-2）=-1
所以函数的值域为[-1，+∞） …（12分）
点评：本题主要考查了偶函数的定义的应用，函数的单调性的定义在证明（判断）函数的单调性中的应用，属于基本知识的简单的应用
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|