题目内容
已知函数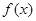 的定义域是
的定义域是 ,
, 是
是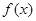 的导函数,且
的导函数,且 在
在 内恒成立.
内恒成立.
(1)求函数 的单调区间;
的单调区间;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)设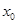 是
是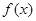 的零点,
的零点, ,求证:
,求证:
【答案】
(1) 的单调区间为
的单调区间为 ;(2)
;(2) ;(3)利用函数的单调性及放缩法证明
;(3)利用函数的单调性及放缩法证明
【解析】
试题分析:(1) ,∵
,∵ 在
在 内恒成立
内恒成立
∴ 在
在 内恒成立,∴
内恒成立,∴ 的单调区间为
的单调区间为 4分
4分
(2)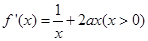 ,∵
,∵ 在
在 内恒成立
内恒成立
∴ 在
在 内恒成立,即
内恒成立,即 在
在 内恒成立,
内恒成立,
设 ,
,
 ,
, ,
, ,
, ,
,
故函数 在
在 内单调递增,在
内单调递增,在 内单调递减,
内单调递减,
∴ ,∴
,∴ 8分
8分
(3)∵ 是
是 的零点,∴
的零点,∴ 由(1),
由(1), 在
在 内单调递增,
内单调递增,
∴当 时,
时, ,即
,即 ,
,
∴ 时
时 ,∵
,∵ ,∴
,∴ ,
,
且 即
即
∴ ,
,
∴ 14分
14分
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 的定义域是[0,2],则函数
的定义域是[0,2],则函数 的定义域是( )
的定义域是( ) C.
C.
 D.
D.

 的定义域是
的定义域是 ,则函数
,则函数 的定义域为
的定义域为
 的定义域是R,若对于任意
的定义域是R,若对于任意 为其定义域上的增函数,则函数
为其定义域上的增函数,则函数